РАЗДЕЛ I. Сущность гуманизма и традиции: филоменологический акцент.

Целой частью числа x называется наибольшее целое число r, не превышающее x.

Целая часть числа x обозначается символом [ x ] или (реже) E (x).

Если x принадлежит интервалу [ r; r +1), где r — целое число, то [ x ]= r, т.е. x находится в интервале [ [ x ]; [ x ]+1). Тогда, по свойствам числовых неравенств, разность x -[ x ] будет в интервале [0; 1). Число q = x - [ x ] называют дробной частью числа x и обозначают { x }. Следовательно, дробная часть числа всегда неотрицательна и не превышает 1, тогда как целая часть числа может принимать как положительные значения, так и неположительные. Таким образом { x } = x - [ x ], а следовательно x = [ x ] + { x }.

Например:

[5]=5	[7,2]=7	[-3]=-3	[-4,2]=-5	[0]=0
{5}=0	{7,2}=0,2	{-3}=0	{-4,2}=0,8	{0}=0

Функция целая часть числа имеет вид y = [ x ].

1. Областью определения является все множество действительных чисел

D([ x ]) = R.

2. Функция ни четная, ни нечетная. Область определения функции симметрична относительно начала координат, но если [ x ] = a, то [- x ] = -(a +1), т.е. не выполняется ни условие четности (f (- x) = f (x)), ни условие нечетности (f (- x) = - f (x)).

3. Функция y = [ x ] не периодическая.

4. Множество значений функции y = [ x ], это множество целых чисел (по определению целой части числа)

E ([ x ]) = Z

5. Функция неограничена, так как множество значений функции — все целые числа, множество целых чисел неограничено.

6. Функция разрывна.

7. Функция принимает значение 0 для всех x, принадлежащих интервалу [0;1), что следует из определения целой части числа. Следовательно, нулями функции будут все значения этого интервала.

8. Учитывая свойства целой части числа функция y = [ x ] принимает отрицательные значения при x меньших нуля, и положительные значения при x больших 1.

9. Функция y = [ x ] кусочно - постоянная и неубывающая.

10. Точек экстремума функция не имеет, так как не меняет характер монотонности.

11. Так как функция y = [ x ] постоянна на каждом интервале [ n; n +1), она не принимает наибольшего и наименьшего значений на области определения.

12. График функции.

 

 

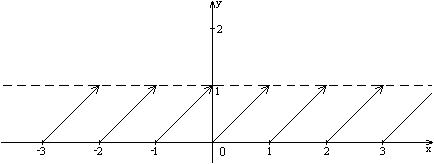
Функция дробная часть числа имеет вид y = { x }.

1. Область определения этой функции все действительные числа

D({ x }) = R.

2. Функция ни четная, ни нечетная. Область определения функции симметрична относительно начала координат, но не выполняется ни условие четности (f (- x) = f (x)), ни условие нечетности (f (- x) = - f (x)).

3. Функция периодическая с наименьшим положительным периодом T = 1.

4. Функция y = { x } принимает значения на интервале [0;1), что следует из определения дробной части числа, т.е.

E({ x }) = [0; 1).

5. Из предыдущего свойства следует, что функция y = { x } ограничена.

6. Функция y = { x } непрерывна на каждом интервале [ n; n +1), где n — целое, в каждой точке n функция терпит разрыв.

7. Функция y = { x } обращается в 0 при всех целых значениях x, что следует из определения функции. То есть нулями функции будут все целочисленные значения аргумента.

8. Функция y = { x } на всей области определения принимает только положительные значения.

9. Функция строго монотонно возрастающая на каждом интервале [ n; n +1), где n — целое число.

10. Точек экстремума функция не имеет, так как не меняет характер монотонности.

11. Учитывая свойства 6 и 9, на каждом интервале [ n; n +1) функция y = { x } принимает минимальное значение в точке n.

12. График функции.

 

РАЗДЕЛ I. Сущность гуманизма и традиции: филоменологический акцент.