Модальное управление.
Системы автоматического управления, как известно, могут быть построены различными способами (методами расчета регуляторов). Самая распространенная схема управления имеет вид:
Рис. 2.18. Управление (регулирование) в данной системе осуществляется по отклонению (e=r-y). Такие регуляторы называются регуляторами 1 рода, то есть регуляторами, в работе которых используется информация об одной переменной (у). Регуляторами 2 рода, или регуляторами состояния, - называются регуляторы, в которых при расчете управляющего воздействия используется все или некоторые переменные состояния. К регуляторам состояния относится модальный регулятор. Модальное управление относится к корневым методам синтеза линейных САУ, то есть исходя из заданных (желаемых, требуемых) показателей качества управления строится желаемый характеристический полином, то есть определяется местоположение корней характеристического уравнения. (Корни на латыни называются моды, отсюда название регулятора – модальный регулятор). Пусть дан объект управления, представленный в виде схемы переменных состояния:
Рис. 2.19. Динамика процесса описывается уравнением:
где R – вектор входных переменных; X – вектор состояния; A – матрица коэффициентов; B – матрица входа. Суть модального регулятора заключается в расчете коэффициентов обратной связи, обеспечивающих заданные показатели качества.
Рис. 2.20. В систему вводится новый входной вектор
Известно, что динамику переходных процессов определяют корни характеристического уравнения поэтому, определяя желаемый характер полинома, можно добиться требуемых показателей качества.
где Таким образом, разрешая систему уравнений (1) относительно неизвестных коэффициентов К, определяются коэффициенты отрицательной обратной связи по вектору состояния Х, которые и представляют собой модальный регулятор.
|



 , (57)
, (57)
 – вектор управляющих, связь которого со старым входным вектором R обеспечивается данным уравнением
– вектор управляющих, связь которого со старым входным вектором R обеспечивается данным уравнением  . Тогда система дифференциальных уравнений, описывающих динамику системы будет иметь вид:
. Тогда система дифференциальных уравнений, описывающих динамику системы будет иметь вид:
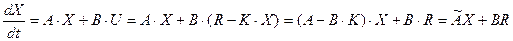 (58)
(58)
 - желаемое характеристическое уравнение, определенное исходя из заданных показателей качества управления по косвенной корневой оценке.
- желаемое характеристическое уравнение, определенное исходя из заданных показателей качества управления по косвенной корневой оценке.


