в евклидовом пространстве
Для дальнейшего изучения евклидовых пространств важно уметь строить в этих пространствах ортонормированные базисы. Как будет показано в следующей теореме, по произвольному базису евклидова пространства всегда можно построить ортонормированный базис. Теорема 3.6. В любом конечномерном евклидовом пространстве существует ортонормированный базис. □ Выберем произвольный базис На первом шаге положим векторы На втором шаге построим вектор
Из условия ортогональности векторов
откуда
Пронормировав его, получим единичный вектор На третьем шаге строим вектор
так, чтобы он был ортогонален векторам
откуда
Пронормировав его, получим единичный вектор Продолжая процесс построения векторов
В силу того, что построенные векторы Рассмотренный выше процесс построения ортонормированного базиса
Рассмотрим на примере процесс ортогонализации Грамма-Шмидта. Пример 3.2. В пространстве
Провести процесс ортогонализации Грама-Шмидта системы векторов базиса Решение. Проведем процесс ортогонализации Грама-Шмидта системы векторов
Итак, ортонормированный базис
|

 в
в 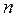 -мерном евклидовом пространстве
-мерном евклидовом пространстве  . Существование искомого ортонормированного базиса
. Существование искомого ортонормированного базиса  в пространстве
в пространстве  ,
,  , причем
, причем 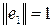 .
. так, чтобы он был ортогонален вектору
так, чтобы он был ортогонален вектору  . Подберем его в виде
. Подберем его в виде .
.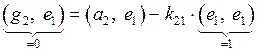 ,
, . Итак, вектор
. Итак, вектор 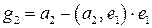 .
. .
.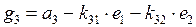
 . Из условия ортогональности векторов
. Из условия ортогональности векторов  и
и 
 Итак, вектор
Итак, вектор 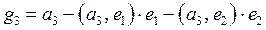 .
.
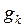 (
( ) при условии, что
) при условии, что  , получим
, получим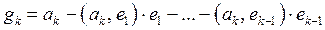 ,
,
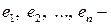 единичные и попарно ортогональные (а значит, линейно независимые), то они образуют ортонормированный базис
единичные и попарно ортогональные (а значит, линейно независимые), то они образуют ортонормированный базис  евклидового пространства. ■
евклидового пространства. ■ ,
, 
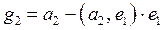
 ,
, 


 ,
, 
 ,
,
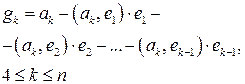
 ,
, 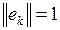 ,
,
 ,
…………….
,
…………….

 со стандартным скалярным произведением
со стандартным скалярным произведением  задан базис
задан базис 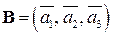 :
: .
. базиса
базиса 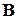 . Согласно предложенной методике решения задачи вычисляем следующие векторы:
. Согласно предложенной методике решения задачи вычисляем следующие векторы: ,
,  ,
, 
 ,
,  ;
; ,
, 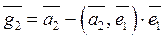
 ,
, ,
,  ,
,  ;
; ,
,  ,
,
 ,
,  ,
, ,
,  .
. состоит из векторов:
состоит из векторов:
 ,
,  .
.


