Определение 3.5. Два вектора  евклидового пространства
евклидового пространства  называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю:
 .
.
Из определения скалярного произведения следует, что нулевой вектор  ортогонален любому вектору
ортогонален любому вектору 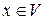 .
.
Определение 3.6. Вектор 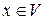 называется ортогональным подпространству
называется ортогональным подпространству  , если он ортогонален каждому вектору этого подпространства.
, если он ортогонален каждому вектору этого подпространства.
Если  , то вектор
, то вектор 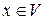 ортогонален подпространству
ортогонален подпространству  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Определение 3.7. Система векторов  евклидова пространства
евклидова пространства  называется ортогональной, если любые её два вектора ортогональны:
называется ортогональной, если любые её два вектора ортогональны:
 ,
,  ,
,  .
.
Теорема 3.5. Любая ортогональная система  ненулевых векторов линейно независима.
ненулевых векторов линейно независима.
□ Составим равенство
 , (3.9)
, (3.9)
где  некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор
некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор  , на основании свойств скалярного произведения получим:
, на основании свойств скалярного произведения получим:
 ,
,
откуда
 .
.
Так как  , то равенство (3.9) примет вид
, то равенство (3.9) примет вид
 , (3.10)
, (3.10)
Умножив равенство (3.10) скалярно на вектор  , получим
, получим  . И так далее. Окончательно получаем, что все коэффициенты
. И так далее. Окончательно получаем, что все коэффициенты 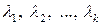 равны нулю. Тогда по определению система ненулевых векторов
равны нулю. Тогда по определению система ненулевых векторов  линейно независима. ■
линейно независима. ■
Теорема 3.6. Если  ортогональная система векторов, то выполняется равенство
ортогональная система векторов, то выполняется равенство
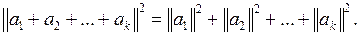 (3.11)
(3.11)
□ Вычислим скалярный квадрат вектора  :
:
 ,
,
откуда и следует равенство (3.11). ■
Пусть далее  – конечномерное (
– конечномерное ( ) евклидово пространство.
) евклидово пространство.
Определение 3.8. Если базис  евклидова пространства
евклидова пространства  представляет собой ортогональную систему векторов:
представляет собой ортогональную систему векторов:
 ,
,  ,
,  ,
,
то он называется ортогональным базисом евклидова пространства  .
.
Определение 3.9. Вектор  называется единичным, если его евклидова норма равна единице:
называется единичным, если его евклидова норма равна единице:
 .
.
Очевидно, что любой ненулевой вектор  можно преобразовать в единичный вектор
можно преобразовать в единичный вектор  следующим образом:
следующим образом:
 .
.
При этом говорят, что вектор  пронормирован, а число
пронормирован, а число  называют нормирующим множителем.
называют нормирующим множителем.
Определение 3.10. Ортогональный базис  евклидова пространства
евклидова пространства  называется ортонормированным, если каждый вектор
называется ортонормированным, если каждый вектор  (
( ) этого базиса – единичный, то есть
) этого базиса – единичный, то есть

Использование ортонормированного базиса облегчает вычисление скалярного произведения в координатной форме. Пусть  – ортонормированный базис и разложение векторов
– ортонормированный базис и разложение векторов  в этом базисе имеет вид
в этом базисе имеет вид
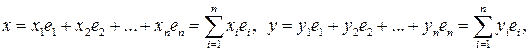
где  координатные вектор-столбцы.
координатные вектор-столбцы.
Матрица Грама для системы векторов  в этом случае имеет вид
в этом случае имеет вид
 .
.
Тогда скалярное произведение (3.5) в ортонормированном базисе  примет наиболее простой вид
примет наиболее простой вид
 . (3.12)
. (3.12)
В ортонормированном базисе также упрощается вычисление координат вектора – они вычисляются через скалярные произведения. Если разложение вектора  по ортонормированному базису
по ортонормированному базису  имеет вид
имеет вид
 ,
,
то умножив обе части последнего равенства скалярно на 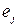 (
( ), получим
), получим
 .
.
Тогда разложение вектора  по ортонормированному базису
по ортонормированному базису  будет иметь вид
будет иметь вид
 .
.

 евклидового пространства
евклидового пространства  называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю: .
. ортогонален любому вектору
ортогонален любому вектору 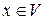 .
. , если он ортогонален каждому вектору этого подпространства.
, если он ортогонален каждому вектору этого подпространства. , то вектор
, то вектор  тогда и только тогда, когда
тогда и только тогда, когда  .
. евклидова пространства
евклидова пространства  ,
,  ,
,  .
. , (3.9)
, (3.9) некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор
некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор  , на основании свойств скалярного произведения получим:
, на основании свойств скалярного произведения получим: ,
, .
. , то равенство (3.9) примет вид
, то равенство (3.9) примет вид , (3.10)
, (3.10) , получим
, получим  . И так далее. Окончательно получаем, что все коэффициенты
. И так далее. Окончательно получаем, что все коэффициенты 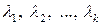 равны нулю. Тогда по определению система ненулевых векторов
равны нулю. Тогда по определению система ненулевых векторов  ортогональная система векторов, то выполняется равенство
ортогональная система векторов, то выполняется равенство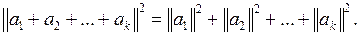 (3.11)
(3.11) :
: ,
, ) евклидово пространство.
) евклидово пространство. евклидова пространства
евклидова пространства  ,
,  ,
, называется единичным, если его евклидова норма равна единице:
называется единичным, если его евклидова норма равна единице: .
. можно преобразовать в единичный вектор
можно преобразовать в единичный вектор  следующим образом:
следующим образом: .
. называют нормирующим множителем.
называют нормирующим множителем. евклидова пространства
евклидова пространства  (
( ) этого базиса – единичный, то есть
) этого базиса – единичный, то есть
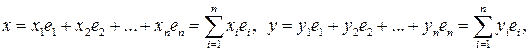
 координатные вектор-столбцы.
координатные вектор-столбцы. в этом случае имеет вид
в этом случае имеет вид .
. примет наиболее простой вид
примет наиболее простой вид . (3.12)
. (3.12) по ортонормированному базису
по ортонормированному базису  ,
,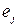 (
( ), получим
), получим .
. .
.


