В евклидовом пространстве обобщением понятия длины вектора является его норма.
Определение 3.2. Функцию, заданную на линейном пространстве  , которая каждому вектору
, которая каждому вектору 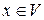 ставит в соответствие действительное число
ставит в соответствие действительное число  , называют нормой вектора, если она удовлетворяет следующим аксиомам:
, называют нормой вектора, если она удовлетворяет следующим аксиомам:

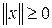 , причем
, причем 
 ;
;

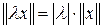 ,
,  ;
;

 , при всех
, при всех  (неравенство треугольника).
(неравенство треугольника).
При этом линейное пространство  , в котором введена норма
, в котором введена норма  , называется нормированным пространством.
, называется нормированным пространством.
Отметим, что евклидовы пространства и нормированные пространства есть линейные пространства с дополнительными структурами – скалярным произведением и нормой соответственно. При этом если в линейном пространстве  введено скалярное произведение, то исходя из этого скалярного произведения можно ввести и норму в этом пространстве, то есть превратить его в нормированное пространство.
введено скалярное произведение, то исходя из этого скалярного произведения можно ввести и норму в этом пространстве, то есть превратить его в нормированное пространство.
Теорема 3.2. Если  – евклидово пространство со скалярным произведением
– евклидово пространство со скалярным произведением 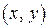 , то
, то  есть нормированное пространство с евклидовой нормой
есть нормированное пространство с евклидовой нормой
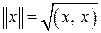 . (3.2)
. (3.2)
□ Докажем, что норма  при помощи формулы (3.2) введена корректно (докажем выполнимость аксиом
при помощи формулы (3.2) введена корректно (докажем выполнимость аксиом  ).
).
Выполнимость аксиомы  следует из аксиомы
следует из аксиомы  определения евклидова пространства.
определения евклидова пространства.
Выполнимость аксиомы  доказывается непосредственно:
доказывается непосредственно:
 ,
,  .
.
Выполнимость аксиомы  доказывается с использованием неравенства Коши-Буняковского, которое выполняется в силу того, что
доказывается с использованием неравенства Коши-Буняковского, которое выполняется в силу того, что  – евклидово пространство:
– евклидово пространство:
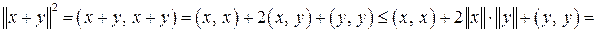
 ■
■
Приведем далее различные способы введения норм в двух евклидовых пространствах 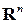 и
и  .
.
Рассмотрим пространство
 .
.
В нем норму определяют одним из четырех способов:
1) Введение нормы через стандартное скалярное произведение (евклидова норма или  -норма):
-норма):
 .
.
2) Введение нормы через скалярное произведение в виде билинейной формы:
 ,
,
где  симметрическая (
симметрическая ( ,
,  ) положительно определенная матрица
) положительно определенная матрица  -го порядка.
-го порядка.
3)  -норма или октаэдрическая норма:
-норма или октаэдрическая норма:
 .
.
4)  -норма или кубическая норма:
-норма или кубическая норма:
 .
.
В пространстве  матриц размера
матриц размера  норму можно вводить различными способами. Наиболее часто используется подход, связанный с введением так называемой индуцированной нормы.
норму можно вводить различными способами. Наиболее часто используется подход, связанный с введением так называемой индуцированной нормы.
Определение 3.3. Если в пространстве 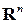 введена норма
введена норма  (см. выше), то индуцированной (подчиненной) нормой в пространстве
(см. выше), то индуцированной (подчиненной) нормой в пространстве  называется
называется
 .
.
При этом норма  в пространстве
в пространстве 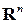 называется порождающей норму в пространстве
называется порождающей норму в пространстве  .
.
Задавая различные нормы в 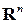 , мы будем получать индуцированные нормы в
, мы будем получать индуцированные нормы в  (см. табл. 3.1).
(см. табл. 3.1).
Таблица 3.1
| №
| Норма  в в 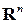
| Индуцированная норма в 
|
|
| евклидова норма
или  -норма -норма

| евклидова норма или  -норма -норма
 .
По-другому называется спектральной нормой .
По-другому называется спектральной нормой
|
|
|  -норма -норма

| максимальная столбцевая или октаэдрическая норма

|
|
|  -норма: -норма:

| максимальная строчная или кубическая норма
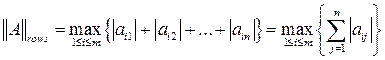
|
Другой подход с введением нормы в пространстве  связан с тем, что это пространство интерпретируют как линейное пространство размерности
связан с тем, что это пространство интерпретируют как линейное пространство размерности  . Тогда можно ввести еще две нормы:
. Тогда можно ввести еще две нормы:
1)  -норма
-норма  ,
,
2)  -норма
-норма  .
.
В пространстве  , элементами которого являются многочлены относительно переменной
, элементами которого являются многочлены относительно переменной  степеней, не превосходящих натуральное число
степеней, не превосходящих натуральное число  :
:
 ,
,
евклидову норму  можно ввести одним из следующих способов:
можно ввести одним из следующих способов:
 ,
,
 ,
,
где  попарно различные действительные числа,
попарно различные действительные числа,  .
.
В любом евклидовом пространстве  можно ввести понятие косинуса угла между двумя векторами. В силу неравенства Коши-Буняковского можно записать неравенство
можно ввести понятие косинуса угла между двумя векторами. В силу неравенства Коши-Буняковского можно записать неравенство
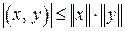 . (3.3)
. (3.3)
Определение 3.3. Углом  между ненулевыми векторами
между ненулевыми векторами  в евклидовом пространстве
в евклидовом пространстве  называется значение от
называется значение от  до
до  , определяемое из равенства
, определяемое из равенства
 . (3.4)
. (3.4)
Заметим, что угол  между ненулевыми векторами
между ненулевыми векторами  определен корректно в силу неравенства (3.3), то есть
определен корректно в силу неравенства (3.3), то есть
 .
.

 , которая каждому вектору
, которая каждому вектору 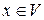 ставит в соответствие действительное число
ставит в соответствие действительное число  , называют нормой вектора, если она удовлетворяет следующим аксиомам:
, называют нормой вектора, если она удовлетворяет следующим аксиомам:
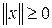 , причем
, причем 
 ;
;
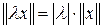 ,
,  ;
;
 , при всех
, при всех  (неравенство треугольника).
(неравенство треугольника).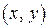 , то
, то 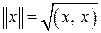 . (3.2)
. (3.2) ).
). следует из аксиомы
следует из аксиомы  определения евклидова пространства.
определения евклидова пространства. доказывается непосредственно:
доказывается непосредственно: ,
,  доказывается с использованием неравенства Коши-Буняковского, которое выполняется в силу того, что
доказывается с использованием неравенства Коши-Буняковского, которое выполняется в силу того, что 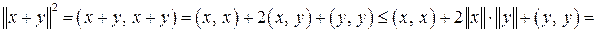
 ■
■ и
и  .
. .
. -норма):
-норма): .
. ,
, симметрическая (
симметрическая ( ,
,  ) положительно определенная матрица
) положительно определенная матрица  -го порядка.
-го порядка. -норма или октаэдрическая норма:
-норма или октаэдрическая норма: .
. -норма или кубическая норма:
-норма или кубическая норма: .
. норму можно вводить различными способами. Наиболее часто используется подход, связанный с введением так называемой индуцированной нормы.
норму можно вводить различными способами. Наиболее часто используется подход, связанный с введением так называемой индуцированной нормы. (см. выше), то индуцированной (подчиненной) нормой в пространстве
(см. выше), то индуцированной (подчиненной) нормой в пространстве  .
.
 .
По-другому называется спектральной нормой
.
По-другому называется спектральной нормой



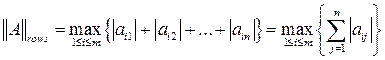
 . Тогда можно ввести еще две нормы:
. Тогда можно ввести еще две нормы: ,
, .
. , элементами которого являются многочлены относительно переменной
, элементами которого являются многочлены относительно переменной  степеней, не превосходящих натуральное число
степеней, не превосходящих натуральное число  ,
, можно ввести одним из следующих способов:
можно ввести одним из следующих способов: ,
, ,
, попарно различные действительные числа,
попарно различные действительные числа,  .
.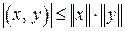 . (3.3)
. (3.3) между ненулевыми векторами
между ненулевыми векторами  до
до  , определяемое из равенства
, определяемое из равенства . (3.4)
. (3.4) .
.


