Зміст лекції. Теплоємності питома та молярна. Рівняння Майера. Ізопроцеси, їхні рівняння.
Теплоемкость. Удельная теплоемкость вещества величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Единица удельной теплоемкости - джоуль на килограмм.кельвин (Дж /(кг.К)). Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:
где n= m / M - количество вещества, выражающее число молей. Единица молярной теплоемкости - джоуль на моль.кельвин (Дж /(моль . К)). Удельная теплоемкость с связана с молярной Сm соотношением Ст = сМ, где М - молярная масса вещества. Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.
Запишем выражение первого начала термодинамики ля 1 моля газа: CmdT=dUm+pdVm. Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моля газа при повышении его температуры на 1 К.
Если газ нагревается при постоянном давлении, то можно записать
Учитывая, что Cp = Cv + R. Это выражение называется уравнением Майера; оно показывает, что Ср всегда больше СV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение Ср к CV (коэффициент Пуассона): g=Cp/CV = (i + 2)/ i. Из выведенных формул следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры (молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы). Применение первого начала термодинамики к изопроцессам. Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы,при которых один из основных параметров состояния сохраняется постоянным.
Как уже указывалось, из первого начала термодинамики (d Q=dU +d A) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: d Q=dU. Но, dUm = CvdT. Тогда для произвольной массы газа получим
Изобарный процес с (р= const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V 1до V 2равна
откуда
Тогда выражение для работы изобарного расширения примет вид
Из этого выражения вытекает физический смысл молярной газовой постоянной R:если T 2- T 1=1 К, то для 1 моля газа R=А, т. е. R численно равна работе изобарного расширения одного моля идеального газа при нагревании его на 1 К. В изобарном процессе при сообщении газу массой m количества теплоты
его внутренняя энергия возрастает на величину
При этом газ совершит работу, определяемую выражением Изотермический процесс (T =const). Процесс описывается законом Бойля-Мариотта: pV =const. Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу (см.рис.60), расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Найдем работу изотермического расширения газа:
Так как при T =const внутренняя энергия идеального газа не изменяется:
то из первого начала термодинамики (d Q = dU+ d A) следует, что для изотермического процесса d Q= d A, т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
Следовательно, для того чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения. Адиабатический процесс. Политропный процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики (d Q=dU+ d A) для адиабатического процесса следует, что d A= -dU т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Для произвольной массы газа перепишем уравнение в виде
Продифференцировав уравнение состояния для идеального газа
Исключим из уравнений температуру Т:
Разделив переменные и учитывая, что Ср/Сv=g, найдем Интегрируя это уравнение в пределах от р 1до p 2и соответственно от V 1до V 2, а затем потенцируя, придем к выражению
Так как состояния 1 и 2 выбраны произвольно, то можно записать . Полученное выражение есть уравнение адиабатического процесса,называемое также уравнением Пуассона. Для перехода к переменным Т, V или р, Т исключим с помощью уравнения Клапейрона-Менделеева
соответственно давление или объем: Все полученные выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина
называется показателем адиабаты (или коэффициентом Пуассона).
Вычислим работу, совершаемую газом в адиабатическом процессе. Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от Т 1до T 2и работа расширения идеального газа Полученное выражение для работы при адиабатическом расширении газа можно преобразовать к виду
где Работа, совершаемая газом при адиабатическом расширении 1 - 2 (определяется площадью, выполненной в цвете на рис.83), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом - температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты. Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность - они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны Cv и Ср,в изотермическом процессе (dT =0) теплоемкость равна
|

 .
. ,
, ,
, ,
, .
. не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, аопределяется лишь температурой Т)и всегда равна СV; продифференцировав уравнение Клапейрона-Менделеева pVm=RT по T (p = const), получим
не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, аопределяется лишь температурой Т)и всегда равна СV; продифференцировав уравнение Клапейрона-Менделеева pVm=RT по T (p = const), получим
 Изохорный процесс (V =const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис.81), где процесс 1 - 2 есть изохорное нагревание, а 1 - 3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е. d A = pdV = 0.
Изохорный процесс (V =const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис.81), где процесс 1 - 2 есть изохорное нагревание, а 1 - 3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е. d A = pdV = 0.

 и определяется площадью прямоугольника на рис.82. Если использовать уравнение Клапейрона-Менделеева для выбранных нами двух состояний, то
и определяется площадью прямоугольника на рис.82. Если использовать уравнение Клапейрона-Менделеева для выбранных нами двух состояний, то ,
, .
.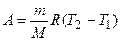 .
.
 .
.
 ,
,
 .
. , noлучим
, noлучим .
. .
. .
. , Или
, Или  .
. ,
,  .
.
 Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис.83). На рисунке видно, что адиабата (pVg=const) более крута, чем изотерма(pV=const). Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис.83). На рисунке видно, что адиабата (pVg=const) более крута, чем изотерма(pV=const). Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры. .
. .
. ,
, .
. , в адиабатическом (d Q =0) теплоемкость равна нулю.
, в адиабатическом (d Q =0) теплоемкость равна нулю.


