Применение теоремы Гаусса к расчету электростатических полей.
E= s/(2eo). Из формулы вытекает, что E не зависит от длины цилиндра, т.с. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
Таким образом, результирующая напряженность поля в области между плоскостями описывается выведенной формулой, а вне объема, ограниченного плоскостями, равна нулю. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис.128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса, 4p r 2 E = Q /eo, откуда
При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости E от r приведен на рис.129. Если r '< R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E =0).
Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E =0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется полученным выражением, внутри же его поле отсутствует. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис.132) перемещается другой точечный заряд Q o, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
Работа при перемещении заряда Q o из точки 1 в точку 2
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы - консервативными. Из полученной формулы следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т. е. Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l = Eldl, где El=E cosa - проекция вектора Е на направление элементарного перемещения. Тогда формулу можно записать в виде
Интеграл ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа. Как показано ранее, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q o в начальной и конечной точках поля заряда Q:
откуда следует, что потенциальная энергия заряда Q o в поле заряда Q равна
Потенциальная энергия, как и в механике, определяется не однозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r
Для одноименных зарядов QoQ>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов QoQ<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна. Если поле создается системой п точечных зарядов Q 1, Q 2,..., Qn, то работа электростатических сил, совершаемая над зарядом Qo, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q o, находящегося в этом поле, равна сумме его потенциальных энергий Ui, создаваемых каждым из зарядов в отдельности:
Из формул вытекает, что отношение U/Q o не зависит от Q o и поэтому является энергетической характеристикой электростатического поля, называемой потенциалом:
|
Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис.126) заряжена с постоянной поверхностной плотностью +s (
- заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания En совпадает с Е), т.е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен sS. Согласно теореме Гаусса, 2 ES = sS/eo, откуда
Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис.127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +s и -s. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние - от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E ++ E _ (E + и Е _определяются по вышеприведенной формуле), поэтому результирующая напряженность поля в вакууме
.
.
Поле объемно заряженного шара. Шаррадиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r (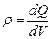
- заряд, приходящийся на единицу объема). Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае. Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд 
. Поэтому, согласно теореме Гаусса,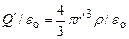 
. Учитывая, что 
, получим
.
Таким образом, напряженность поля вне равномерно заряженного тара описывается вышеприведенной формулой, а внутри его изменяется линейно с расстоянием. График зависимости E от r приведен на рис.130. Поле равномерно заряженного бесконечного цилиндра (нити). 
Бесконечный цилиндр радиуса R (рис.131) заряжен равномерно с линейной плотностью t (
- заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора E сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность -2p rlЕ. По теореме Гаусса, при r>R 2p rlE= t l /eo, откуда
.
.
Так как dl cosa= dr, то 
.
.
.
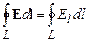называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности Е электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность. Данный вывод справедлив только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов циркуляция вектора напряженности Е отлична от нуля.
,
.
) потенциальная энергия обращается в нуль (U =0), то С =0 и потенциальная энергия заряда Q o, находящегося в поле заряда Q на расстоянии r от него, равна
.
.
.
