РЕАЛЬНІ ГАЗИ.
Зміст лекції. Рівняння Ван-дер-Ваальсу. Внутрішня енергія реального газу. Дросель-ефект. Зрідження газів. Силы и потенциальная энергия межмолекулярного взаимодействия. Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяет описывать поведение разреженных реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними. Так, в 1 м 3 газа при нормальных условиях содержится 2,68 1025 молекул, занимающих объем примерно 10-4 м 3 (радиус молекулы примерно 10-10 м ), которым по сравнению с объемом газа (1 м 3) можно пренебречь. При давлении 500 МПа (1 атм =101,3 кПа) объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна.
В XX в., по мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис.88, а приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где F oи Fn - соответственно силы отталкивания и притяжения, a F - их результирующая. Силы отталкивания считаются положительными, асилы взаимного притяжения - отрицательными. На расстоянии r=r o результирующая сила F=0,т.е. силы притяжения и отталкивания уравновешивают друг друга. Таким образом, расстояние r о соответствует равновесному расстоянию между молекулами, на котором бы они находились в отсутствие теплового движения. При r < r o преобладают силы отталкивания (F >0), при r > r o - силы притяжения (F <0). На расстояниях r >10-9 м межмолекулярные силы взаимодействия практически отсутствуют ( Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис.88, б)следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют Критерием различных агрегатных состояний вещества является соотношение величин Pmin и kT. Pmin - наименьшая потенциальная энергия взаимодействия молекул - определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии (r=rо);kT определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического теплового движения молекул. Если Pmin<< kT, то вещество находится в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния r o, т. е. вероятность образования агрегатов из молекул достаточно мала. Если P min>>kT,то вещество находится в твердом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого r о. Если Пmin Например, у инертных газов Pmin мало, а у металлов - велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях. Уравнение Ван-дер-Ваальса. Для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона-Менделеева pVm=RT (для моля газа), описывающее идеальный газ, для реальных газов непригодны. Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837-1923) вывел уравнения состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона-Менделеева введены две поправки. 1.Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm,a Vm - b, где b - объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т.е. объем, равный восьми объемам молекулы, а в расчете на одну молекулу - учетверенный объем молекулы. 2.Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т.е.
где а - постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, V m - молярный объем. Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов): . Для произвольного количества вещества v газа (n= m / M) с учетом того, что V =n Vm, уравнение Ван-дер-Ваальса примет вид
или
где поправки а и b - постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b). При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа. Изотермы Ван-дер-Ваальса и их анализ. Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду
Это уравнение при заданных р и Т является уравнением третьей степени относительно Vm; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1, V 2и V зотвечают (символ «m» для простоты опускаем) одному значению давления p 1), второму случаю - изотермы при высоких температурах.
Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского ученого Т.Эндрюса (1813-1885), изучавшего изотермическое сжатие углекислого газа. Отличие экспериментальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором - волнообразные. Для нахождения критических параметров подставим их значения в уравнение и запишем
(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны V к, уравнение приводится к виду или Так как эти уравнения тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать
Решая полученные уравнения, найдем: V к=3 b, p к= a /(27 b 2), T к=8 a /(27 Rb).
При достаточно низких температурах изотерма пересекает ось Vm,переходя в область отрицательных давлений (нижняя кривая на рис.92). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8 - 9 на нижней изотерме соответствует перегретой жидкости, участок 9-10 - растянутой жидкости. Внутренняя энергия реального газа. Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (определяет внутреннюю энергию идеального газа, равную CvT) и потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ: Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, как известно из механики, идет на увеличение потенциальной энергии системы, т. е. d A=p'dVm =dP или (постоянная интегрирования принята равной нулю). Знак минус означает, что молекулярные силы, создающие внутреннее давление р', являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа
растет с повышением температуры и увеличением объема. Если газ расширяется без теплообмена с окружающей средой (адиабатический процесс, т. е. d Q =0) и не совершает внешней работы (расширение газа в вакуум, т. е. d А =0), то на основании первого начала термодинамики (d Q = (U 2- U 1)+d A) получим, что U 1 =U 2. Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется. Этот вывод формально справедлив как для идеального, так и для реального газов, но физически для обоих случаев совершенно различен. Для идеального газа равенство U 1 =U 2означает равенство температур (Т 1 =Т 2),т.е. при адиабатическом расширении идеального газа в вакуум его температура не изменяется. Для реального газа, учитывая, что для моля газа
получаем
Так как V 2 >V 1, то Т 1> Т 2, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. При адиабатическом сжатии реальный газ нагревается. Резюме -Якщо за цикл здійснюється позитивна робота (цикл протікає за годинниковою стрілкою), то він називається прямим, якщо за цикл здійснюється негативна робота (цикл протікає проти годинникової стрілки), то він називається зворотним.
|

 При рассмотрении реальных газов - газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях
При рассмотрении реальных газов - газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях  10-9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
10-9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими. .Элементарная работа d А силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е. d A=Fdr=-d P.
.Элементарная работа d А силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е. d A=Fdr=-d P.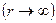 , то P=0. При постепенном сближении молекул между ними появляются силы притяжения (F <0), которые совершают положительную работу (dA=Fdr>;0). Тогда, потенциальная энергия взаимодействия уменьшается, достигая минимума при r=r о.При r < r о с уменьшением r силы отталкивания (F >0) резко возрастают и совершаемая против них работа отрицательна (dA=Fdr<;0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r о) обладает минимальной потенциальной энергией.
, то P=0. При постепенном сближении молекул между ними появляются силы притяжения (F <0), которые совершают положительную работу (dA=Fdr>;0). Тогда, потенциальная энергия взаимодействия уменьшается, достигая минимума при r=r о.При r < r о с уменьшением r силы отталкивания (F >0) резко возрастают и совершаемая против них работа отрицательна (dA=Fdr<;0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r о) обладает минимальной потенциальной энергией. kT, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r о. Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения Pmjn для данного вещества.
kT, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r о. Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения Pmjn для данного вещества. ,
, ,
,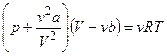 ,
, Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса - кривые зависимости р от Vm при заданных Т,определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис.89) имеют довольно своеобразный характер. При высоких температурах (T > T к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T к на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической,соответствующая ей температура T к - критической температурой. Критическая изотерма имеет лишь одну точку перегиба К,называемую критической точкой;в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V ки давление р к называются также критическими. Состояние с критическими параметрами (р к, V к, Т к) называется критическим состоянием. При низких температурах (Т < Т к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса - кривые зависимости р от Vm при заданных Т,определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис.89) имеют довольно своеобразный характер. При высоких температурах (T > T к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T к на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической,соответствующая ей температура T к - критической температурой. Критическая изотерма имеет лишь одну точку перегиба К,называемую критической точкой;в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V ки давление р к называются также критическими. Состояние с критическими параметрами (р к, V к, Т к) называется критическим состоянием. При низких температурах (Т < Т к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь. .
. Рассматривая различные участки изотермы при T < T к (рис.90), видим, что на участках 1 - 3 и 5-7 при уменьшении объема Vm давление р возрастает, что естественно. На участке 3-5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3-5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 - 6 - 2-1. Часть 7-6 отвечает газообразному состоянию, а часть 2 - 1 - жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6-2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром,а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
Рассматривая различные участки изотермы при T < T к (рис.90), видим, что на участках 1 - 3 и 5-7 при уменьшении объема Vm давление р возрастает, что естественно. На участке 3-5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3-5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 - 6 - 2-1. Часть 7-6 отвечает газообразному состоянию, а часть 2 - 1 - жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6-2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром,а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
 ,
, .
.
 Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис.91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р, Vm под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа - область пара. Пар отличается от остальных газообразных состояний тем, что при изотермичес-ком сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис.91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р, Vm под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа - область пара. Пар отличается от остальных газообразных состояний тем, что при изотермичес-ком сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении. Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2-6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5-6 и 2-3. Эти неустойчивые состояния называются метастабильными. Участок 2-3 изображает перегретую жидкость, 5-6 - пересыщенный пар. Обе фазы ограниченно устойчивы.
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2-6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5-6 и 2-3. Эти неустойчивые состояния называются метастабильными. Участок 2-3 изображает перегретую жидкость, 5-6 - пересыщенный пар. Обе фазы ограниченно устойчивы. .
. ,откуда
,откуда 
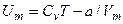
 ,
, .
.


