Ускорения характерных точек кривошипного вала
Ускорение точки В, принадлежащей кривошипу АВ, определим методом решения векторного уравнения (рис.1.1)
где
Направление этих векторов указано под слагаемыми уравнения (1.7). В дальнейшем в векторных уравнениях будем обозначать: если слагаемое подчеркнуть двумя линиями, то это означает, что вектор известен по величине и направлению, а одной линией – вектор известен по направлению. Выбираем масштаб ускорений
где p – полюс плана ускорений. Решив уравнение (1.7), графически определяем абсолютное ускорение точки В:
1.5.2. Расчёт ускорений характерных точек структурных групп II класса методом планов ускорений В образовании плоских многозвенных рычажных механизмов чаще всего используются двухзвенные структурные группы с двумя внешними и одной внутренней одноподвижными кинематическими парами. Одна из внешних кинематических пар этой группы используется для шарнирного соединения с кривошипом или каким-либо другим подвижным звеном механизма. Вторая свободная пара используется для соединения группы со стойкой. Если присоединение группы к стойке осуществлено при помощи вращательной кинематической пары, то ускорение геометрического центра шарнира равно нулю. Если для присоединения группы к стойке использована поступательная пара, то линия действия вектора ускорения совпадает с направляющей для ползуна. Исходя из этих предпосылок задача кинематического исследования сводится к определению ускорения внутренней кинематической пары каждой структурной группы. Методика решения таких задач включает: - составление уравнений связи между кинематическими параметрами узловых точек каждого звена, входящего в структурную группу; - графическое решение этих уравнений применительно к выбранному положению механизма методом построения планов скоростей и ускорений; - расшифровку планов и анализ полученных результатов. Если в точке В к кривошипу АВ присоединить структурную группу с внутренней вращательной кинематической парой в точке С, то уравнение связи между ускорениями этих точек будет иметь следующий вид: а) для шатунно-поршневой группы (рис. 1.2)
б) для шатунно-коромысловой группы (рис. 1.3)
Если в точке В к кривошипу присоединить кулисную группу с внутренней поступательной кинематической парой, то точка В1 кривошипа АВ, точка В2 ползуна 2 и точка В3 кулисы ВД в данный момент геометрически совпадут и уравнения связи между ускорениями этих точек примут следующий вид (рис. 1.4):
а) для точки В1 кривошипа АВ
б) для точки В2 ползуна 2, образующего с кривошипом АВ вращательную кинематическую пару,
в) для точки В3, принадлежащей кулисе 3 и образующей с ползуном 2 поступательную кинематическую пару
г) для точки В3, принадлежащей кулисе 3, вращающейся вокруг неподвижного шарнира Д,
В уравнениях (1.9 – 1.15) приняты условные обозначения: - две горизонтальные черты под слагаемым означают, что вектор определён по величине и направлению; - одна горизонтальная линия под слагаемым означает, что известна только линия действия вектора; величина и направление этого вектора определяются только после графического решения векторного уравнения; - знаки параллельности (||) и перпендикулярности (^) указывают на линию действия вектора по отношению к осевой линии рассматриваемого звена механизма; - в индексе символа нормального ускорения первая буква означает, с какой точкой звена механизма совпадает начало, а вторая буква – к какой точке этого звена направлено острие вектора. Например, в уравнениях (1.9, 1.10) символика означает, что вектор нормального ускорения точки С во вращательном движении вокруг точки В приложен к точке С и направлен к точке В шатуна ВС. Величина вектора нормального ускорения какой-либо точки K во вращательном движении звена KL вокруг точки L определяется по формуле
На плане ускорений величина этого вектора изображается отрезком
где i – номер звена KL на схеме механизма. Угловая скорость i-го звена определяется по формуле
где Численное значение Кориолисова ускорения в уравнении (1.14) определяется по формуле
где
где Направление Кориолисова ускорения совпадает с направлением вектора На плане ускорений этот вектор изображается отрезком (см. рис. 1.4,в)
Методика построения планов ускорений подробно рассмотрена в учебной литературе [1, с. 79–96], [2, с. 84–92] и др. В качестве примера построение плана ускорений приведено: по уравнениям (1.7) и (1.9) на рис. 1.2, в; по уравнениям (1.7) и (1.10, 1.11) на рис. 1.3, б; по уравнениям (1.7) и (1.12–1.15) на рис. 1.4, в. Если точка Si принадлежит звену KL, то её расположение на отрезке (k l) плана ускорений определяется из соотношения, составленного по теореме подобия,
где KL – длина отрезка, изображающего i-е звено на кинематической схеме механизма, мм; KSi– расстояние от точки K до точки Si на отрезке KL, мм; k l – расстояние между точками k и l на плане ускорений, мм; ksi– расстояние от точки k до точки si на плане ускорений, мм. Величина и направление абсолютного ускорения точки S i-го звена механизма определяются отрезком (psi), соединяющим точку Si c полюсом плана ускорений (см. рис. 1.2, в; 1.3, б и 1.4, в). Из плана ускорений касательные ускорения узловых точек и угловые ускорения звеньев определяются по следующим формулам:
где (nik) – длина отрезка, изображающего вектор касательного ускорения звена KL на плане ускорений, мм; l kl – истинная длина i-го звена механизма, м. Ускорение масс центра i-го звена механизма определяется по формуле
где (psi) – расстояние от полюса до точки si отрезка (k l) плана ускорений, мм. Определив по формулам (1.23) и (1.24) величину угловых ускорений центров масс звеньев, следует их направление указать на кинематической схеме механизма (см. рис.1.2,а–1.4,а) и приступить к расчёту сил инерции и моментов инерции звеньев механизма.
1.6. Силы инерции звеньев механизма
Силы инерции – это силы, распределенные по всей длине звена. Для упрощения уравнений и удобства их решения силы инерции приводятся к главному вектору и главному моменту:
где mi – масса i-го звена, кг; Isi– момент инерции i-го звена относительно оси, проходящей через центр масс, кг×м2;
Из уравнений (1.25) следует, что главный вектор Звенья плоских рычажных механизмов могут совершать поступательное, вращательное или плоскопараллельное движения. В зависимости от вида движения и расположения центра масс на звене силы инерции приводятся к главному вектору и главному моменту: a) если звено совершает возвратно-поступательное движение (ползун), то силы инерции приводятся к главному вектору
б) если звено совершает вращательное движение вокруг оси, проходящей через центр масс (кривошип), то силы инерции приводятся к главному моменту
в) если звено совершает плоскопараллельное движение или вращательное движение вокруг оси, не проходящей через центр масс (кулиса, коромысло, шатун), то силы инерции приводятся к главному вектору и главному моменту:
где mi, Isi – масса и момент инерции звена относительно оси, проходящей через центр масс;
Силы тяжести звеньев определяются по формуле
где g = 9,81» 10 м/с2 – ускорение свободного падения. В заданиях на курсовое проектирование чаще всего массой кривошипа пренебрегают, поэтому Рi = 0. Однако в расчетах следует учитывать массу маховика, который устанавливается на кривошип. Если модуль сил тяжести или других сил не превышает 5% от модуля наибольшей силы, действующей на рассматриваемую структурную группу, то этими силами в расчетах следует пренебречь. Определенные таким образом силы прикладывают к соответствующим точкам звеньев структурной группы, вычерченной в соответствующем положении в масштабе μl.
1.7. Реакции кинематических пар
В образовании плоских рычажных механизмов используются вращательные и поступательные кинематические пары. Из теоретической механики известно, что сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности. В поступательной паре сила (реакция) R12 приложена к звену 2 от звена 1, и направлена по нормали n–n к поверхности соприкосновения звеньев (рис. 1.5,а). Модуль реакции R12 и расстояние b неизвестны и должны быть определены в процессе силового расчета. Во вращательной паре без учета сил трения реакция R12 направлена нормально к цилиндрической поверхности соприкосновения звеньев, т.е. проходит через центр шарнира О (рис. 1.5,б). Положение центра шарнира всегда известно, но модуль реакции R12 и угол β неизвестны. Для упрощения расчетов реакции удобно представлять в виде двух составляющих: Rn12 – нормальной составляющей, направленной вдоль рассматриваемого звена, и Rτ12 – касательной составляющей, направленной перпендикулярно рассматриваемому звену. В этом случае реакции Rn12 и Rτ12 будут неизвестны только по величине. Следовательно, от каждой реакции, действующей в любой кинематической паре, в расчетных уравнениях появляются две неизвестные величины, которые определяются в процессе силового расчета.
1.8. Определение реакций в кинематических парах механизма
Для определения реакций в кинематических парах надо предварительно разложить механизм на структурные группы. Каждая структурная группа вычерчивается отдельно в масштабе μl и к ее звеньям прикладываются соответствующие силы. Силовой расчет механизма начинают с определения давлений в кинематических парах структурной группы, наиболее удаленной от входного звена. Определение реакций в кинематических парах рассмотрим на следующих примерах. Кривошипно-шатунный механизм одноступенчатого компрессора (см.рис. 1.2, а). В рассматриваемом примере имеется одна структурная группа, состоящая из звеньев 2 – 3 (рис. 1.2, г). Воздействие входного звена 1 и стойки 0 на звенья отсоединенной группы 2–3 заменяем силами реакций (см. рис. 1.2, г). Одну из составляющих реакций вращательных кинематических пар удобно разложить по направлению звеньев, а вторую – перпендикулярно. Например, R12 представим как сумму векторов двух составляющих:
Первая цифра индекса показывает номер действующего звена, а вторая – номер звена, на которое производится действие. Например, R12 – сила давления первого звена на второе, R03 – действие стойки 0 на ползун 3. В соответствии с принципом Даламбера условие равновесия структурной группы 2–3 имеет следующий вид:
Это уравнение имеет три неизвестных:
Так, если при решении уравнения (1.32) реакция Величину векторов
Модуль реакций R12, R03 и R32 определяется из плана сил (см.рис.1.2,д) по следующим формулам:
Определение реакций в кинематических парах группы Ассура II класса 1-го вида (ВВВ). Рассмотрим данный вопрос на примере соломонабивателя зерноуборочного комбайна (см. рис. 1.3). Пусть даны силы тяжести G2 и G3 звеньев 2 и 3; сила полезного сопротивления РПС; моменты инерции Вычисляем силы инерции (главные векторы РИ и главные моменты сил инерции МИ) по следующим формулам:
где
Силы инерции Реакции во внешних парах В и О3 разложим на две составляющие, направленные по осям звеньев 2 и 3 и перпендикулярно к этим осям, и обозначим их соответственно через
Из этого уравнения находим
Отсюда находим Нормальные составляющие
В этом уравнении все силы, кроме Уравнение (1.38) решаем графически, строя план сил в некотором масштабе Для определения реакций в шарнире С решаем графически векторное уравнение сил, приложенных к одному из звеньев, например к звену 2. Отбрасываем звено 3 и его действие заменяем реакцией
Определение реакций в кинематических парах кулисной структурной группы. Этот вопрос рассмотрим на примере механизма строгального станка (рис.1.4). Данный механизм состоит из двух групп Ассура II класса 4-го (звенья 4–5) и 3-го вида (звенья 2–3). Рассмотрим особенности силового расчета группы Ассура, состоящей из звеньев (4–5) (рис.1.4, г). Это группа образована двумя ползунами, соединенными между собой поступательной кинематической парой. На данную структурную группу действуют следующие силы: тяжести звена 5 G5, полезного сопротивления РПС и инерции звена 5 Р5. Масса звена 4 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G4 = 0 и Р4 = 0. Исполнительное звено (ползун 5) образуют со стойкой поступательную пару в точке Е¢ и дублирующую в точке Е². Реакции этих пар приводятся к равнодействующей R05, приложенной в точке Е². В точке С свободной (внешней) парой является вращательная, соединяющая ползун 4 с кулисой 3. В общем случае реакция R34 этой пары не известна по величине и направлению. Направление реакции R34 установим, рассмотрев равновесие звена 4 (рис.1.4,е). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R34 и R54. Эти силы равны и противоположно направлены. Действия направляющей звена 5 на звено 4 заменим реакцией R54. Известно, что без учета сил трения направление реакции R54 перпендикулярно к направляющим ползуна 4, следовательно и реакция R34 во вращательной кинематической паре будет иметь такое же направление. Уравнение равновесия структурной группы (4–5) имеет следующий вид:
где F5 – главный вектор сил инерции ползуна 5, рассчитанный по формуле (1.26). В данном векторном уравнении неизвестными являются только две силы R05 и R34, поэтому его решение выполним графически методом построения плана сил (рис. 1.4, д). Определение реакций в кинематических парах групп Ассура II класса 3-го вида (рис. 1.4, ж). Эта группа находится в равновесии под действием внешних сил: R43 = –R34, величина и направление которой определены из предыдущих расчетов; силы тяжести G3 звена 3; силы инерции и момента сил инерции звена 3, расчёт которых выполняется по зависимостям (1.28). Масса звена 2 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G2 = 0, Р2 = 0. Реакции, подлежащие определению: R12 – приложенная в центре шарнира А и R03 – приложенная в центре шарнира Д. Составим уравнение равновесия структурной группы (2–3) под действием внешних сил:
Это векторное уравнение можно решить графически, если предварительно найти модуль силы R12. Направление реакции R12 находим, рассмотрев равновесие звена 2 (рис. 1.4,и). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R12 и R32. Значит, эти силы равны и противоположно направлены. Известно, что без учета сил трения реакция R32 направлена перпендикулярно к направляющей СД ползуна 2. Зная направление R12, найдем её модуль из уравнения моментов всех сил относительно точки Д:
откуда находим R12. Уравнение (1.41) решаем графически методом построения плана сил. Реакция R03 замыкает силовой многоугольник, построенный по уравнению (1.41).
1.9. Расчёт входного звена
Механизмы целого ряда двигателей и рабочих машин представляют собой не простые, а разветвленные кинематические цепи. Например, кривошипно-ползунные механизмы двухцилиндровых двигателей внутреннего сгорания. При силовом расчете этих механизмов нужно рассмотреть вначале группу Ассура, состоящую из звеньев 4–5, а затем из звеньев 2–3 аналогично примеру (см. рис. 1.2, а). В результате этих расчетов определяем реакции в кинематических парах В1 (2–1) и В (4–1) шатун-кривошип, т.е. R21 и R41. Кроме реакций R21 и R41 на кривошип действуют силы: GM – сила тяжести маховика, Н; P41 – главный вектор сил инерции кривошипа вместе с маховиком; если ось вращения маховика совпадает с осью вращения кривошипа и кривошип уравновешен, то P41 = (m1 + m2) ×
где IM – момент инерции маховика, кг×м2; e1 – угловое ускорение кривошипа в рассматриваемом положении механизма, с-2; R01 – неизвестная по величине и направлению сила воздействия неподвижной опоры А на кривошип; эта сила на рис. 1.6,а и 1.6,б условно указана пунктирным вектором. В расчётах численные значения параметров GM, IM и e1 принимаются по результатам динамического анализа машинного агрегата. При расчёте схемы рабочей машины на кривошипный вал со стороны приводного двигателя действует неизвестная движущая сила РД.
Рис. 1.6. Расчетные схемы: а – простого; б – разветвленного кривошипа; в, г – планы сил соответственно простого и разветвленного кривошипа.
При расчёте схемы двигателя внутреннего сгорания на кривошипный вал со стороны рабочей машины действует неизвестная сила полезного сопротивления РС. Под действием рассмотренной системы сил кривошипный вал не находится в равновесии (при структурном анализе входного звена установлено, что степень подвижности W = 1). Для уравновешивания кривошипного вала в точке В (см.рис.1.6,а) или в одной из точек В или В1 (см.рис.1.6,б) следует перпендикулярно кривошипу АВ приложить уравновешивающую силу РУР, равную: а) РУР = РД – при расчёте схемы рабочей машины; б) РУР = РС – при расчёте схемы двигателя внутреннего сгорания. Направление вектора РУР следует принять таким, чтобы момент силы МУР = РУР × l AB (1.44) препятствовал вращению кривошипа вокруг точки А под действием сил R41 и R21 и момента
Решение уравнения (1.45) осуществляется построением плана сил в масштабе mp (рис.1.6 в,г). Из плана сил определяется реакция R01: R01 = [R01] × mp.
|

 Рис.1.1. Кинематический анализ ведущего звена: а – схема звена; б – план скоростей; в – план ускорений.
Рис.1.1. Кинематический анализ ведущего звена: а – схема звена; б – план скоростей; в – план ускорений.
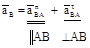 , (1.7)
, (1.7)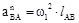 – величина вектора нормального ускорения точки В во вращательном движении вокруг точки А; этот вектор всегда направлен к оси вращения в любом положении механизма;
– величина вектора нормального ускорения точки В во вращательном движении вокруг точки А; этот вектор всегда направлен к оси вращения в любом положении механизма;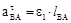 – величина вектора касательного ускорения; этот вектор всегда направлен перпендикулярно кривошипу АВ в любом положении механизма.
– величина вектора касательного ускорения; этот вектор всегда направлен перпендикулярно кривошипу АВ в любом положении механизма.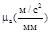 и находим длину отрезков, изображающих на плане ускорений вектора
и находим длину отрезков, изображающих на плане ускорений вектора 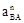 и
и 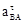 (см. рис.1.1, в), по следующим формулам:
(см. рис.1.1, в), по следующим формулам: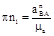 ;
; 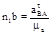 , (1.8)
, (1.8)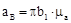 .
. Рис.1.2. Силовой расчет кривошипно-шатунного механизма:
а – кинематическая схема механизма; б – план скоростей; в – план ускорений;
г – расчетная схема группы 2–3; д – план сил группы Аcсура 2–3;
е – расчетная схема входного звена; ж – план сил входного звена.
Рис.1.2. Силовой расчет кривошипно-шатунного механизма:
а – кинематическая схема механизма; б – план скоростей; в – план ускорений;
г – расчетная схема группы 2–3; д – план сил группы Аcсура 2–3;
е – расчетная схема входного звена; ж – план сил входного звена.
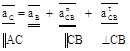 ; (1.9)
; (1.9) Рис.1.3. Силовой расчет группы типа ВВВ:
а – расчетная схема группы; б – план ускорений; в– план сил группы.
Рис.1.3. Силовой расчет группы типа ВВВ:
а – расчетная схема группы; б – план ускорений; в– план сил группы.
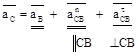 ; (1.10)
; (1.10)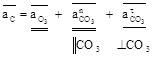 . (1.11)
. (1.11) Рис.1.4. Силовой расчет кривошипно-кулисного механизма:
а) – кинематическая схема механизма; б) – план скоростей; в) – план ускорений;
г) – расчетная схема группы 4–5; д) – план сил группы 4–5;
е) – расчетная схема ползуна 4; ж) – расчетная схема группы 2–3;
з) – план сил группы 2–3; и) – расчетная схема ползуна 2.
Рис.1.4. Силовой расчет кривошипно-кулисного механизма:
а) – кинематическая схема механизма; б) – план скоростей; в) – план ускорений;
г) – расчетная схема группы 4–5; д) – план сил группы 4–5;
е) – расчетная схема ползуна 4; ж) – расчетная схема группы 2–3;
з) – план сил группы 2–3; и) – расчетная схема ползуна 2.
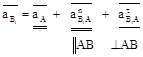 ; (1.12)
; (1.12)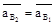 ; (1.13)
; (1.13)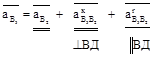 ; (1.14)
; (1.14)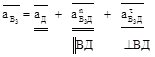 . (1.15)
. (1.15) . (1.16)
. (1.16)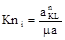 , (1.17)
, (1.17) , (1.18)
, (1.18) – аналог угловой скорости i-го звена в заданном положении механизма.
– аналог угловой скорости i-го звена в заданном положении механизма.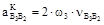 , (1.19)
, (1.19)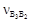 – скорость движения ползуна относительно кулисы 3;
– скорость движения ползуна относительно кулисы 3; , (1.20)
, (1.20)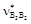 – аналог относительной скорости ползуна.
– аналог относительной скорости ползуна. , повёрнутого на 90° в сторону вращения кулисы.
, повёрнутого на 90° в сторону вращения кулисы.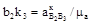 . (1.21)
. (1.21) или
или 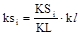 , (1.22)
, (1.22)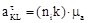 ;
; 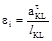 , (1.23)
, (1.23)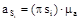 , (1.24)
, (1.24) ;
; 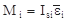 , (1.25)
, (1.25)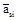 – ускорение центра масс i-го звена, м/c2;
– ускорение центра масс i-го звена, м/c2;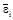 – угловое ускорение i-го звена, с-2.
– угловое ускорение i-го звена, с-2. приложен к центру масс S звена и направлен противоположно вектору ускорения центра масс. Главный момент Мi направлен противоположно угловому ускорению звена.
приложен к центру масс S звена и направлен противоположно вектору ускорения центра масс. Главный момент Мi направлен противоположно угловому ускорению звена.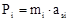 ; (1.26)
; (1.26)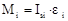 ; (1.27)
; (1.27)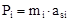 ;
; 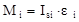 , (1.28)
, (1.28) , ei – ускорение центра масс и угловое ускорение звена.
, ei – ускорение центра масс и угловое ускорение звена.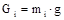 , (1.29)
, (1.29)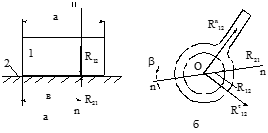 Рис.1.5. Направление реакций кинематических пар:
а – поступательная; б – вращательная.
Рис.1.5. Направление реакций кинематических пар:
а – поступательная; б – вращательная.
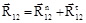 . (1.30)
. (1.30)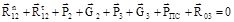 . (1.31)
. (1.31)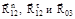 . Реакцию
. Реакцию 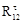 следует определить из уравнения моментов сил, действующих на звено 2, составленного относительно шарнира С.
следует определить из уравнения моментов сил, действующих на звено 2, составленного относительно шарнира С.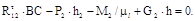 (1.32)
(1.32)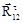 будет иметь положительное значение, то её направление будет совпадать с направлением, указанным на чертеже (см.рис.1.2,г). Если реакция
будет иметь положительное значение, то её направление будет совпадать с направлением, указанным на чертеже (см.рис.1.2,г). Если реакция 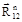 и
и  определяем построением плана сил в масштабе μР по уравнению (1.31) (рис.1.2,д). Построение плана сил следует начинать с реакции
определяем построением плана сил в масштабе μР по уравнению (1.31) (рис.1.2,д). Построение плана сил следует начинать с реакции 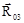 , а через начало реакции
, а через начало реакции 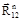 . Линии действия реакции
. Линии действия реакции 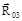 проводятся до их взаимного пересечения. Векторы сил
проводятся до их взаимного пересечения. Векторы сил 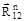 и
и  направляются так, чтобы многоугольник сил был замкнутым. При таком построении легко определить давление в промежуточном шарнире кинематической пары С по уравнению
направляются так, чтобы многоугольник сил был замкнутым. При таком построении легко определить давление в промежуточном шарнире кинематической пары С по уравнению . (1.33)
. (1.33)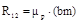 ;
;  ;
;  (1.34)
(1.34) и
и  относительно осей, проходящих через центры масс звеньев 2 и 3. Определим реакции в кинематических парах В, С, О3.
относительно осей, проходящих через центры масс звеньев 2 и 3. Определим реакции в кинематических парах В, С, О3.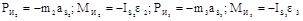 , (1.35)
, (1.35)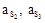 – линейные ускорения центров масс звеньев 2 и 3, определяемые из планов ускорений (см. рис. 1.3,б);
– линейные ускорения центров масс звеньев 2 и 3, определяемые из планов ускорений (см. рис. 1.3,б);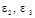 – угловые ускорения звеньев 2 и 3.
– угловые ускорения звеньев 2 и 3. и
и 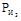 прикладываем в точках S2 и S3 (см. рис.1.3,а) противоположно векторам
прикладываем в точках S2 и S3 (см. рис.1.3,а) противоположно векторам  и
и 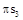 (см. рис.1.3,б). Моменты от пар сил инерции М2 и М3 направляем противоположно угловым ускорениям
(см. рис.1.3,б). Моменты от пар сил инерции М2 и М3 направляем противоположно угловым ускорениям 
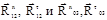 . Тангенциальные составляющие находим из уравнений моментов всех сил относительно точки С для каждого звена в отдельности. Для звена 2 имеем:
. Тангенциальные составляющие находим из уравнений моментов всех сил относительно точки С для каждого звена в отдельности. Для звена 2 имеем: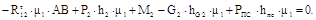 (1.36)
(1.36)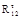 . Аналогично составляем уравнение моментов для звена 3:
. Аналогично составляем уравнение моментов для звена 3: (1.37)
(1.37)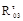 . Все плечи сил в уравнения моментов подставляем в миллиметрах, взяв их непосредственно с чертежа.
. Все плечи сил в уравнения моментов подставляем в миллиметрах, взяв их непосредственно с чертежа.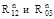 определяем, решая графически векторное уравнение равновесия структурной группы (звенья 2–3):
определяем, решая графически векторное уравнение равновесия структурной группы (звенья 2–3):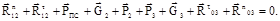 (1.38)
(1.38)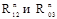 , известны и по величине, и по направлению. Реакции
, известны и по величине, и по направлению. Реакции 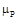 (рис. 1.3, в). Для этого последовательно откладываем все известные силы, перенося их из плана группы на план сил параллельно самим себе. Затем из начала вектора
(рис. 1.3, в). Для этого последовательно откладываем все известные силы, перенося их из плана группы на план сил параллельно самим себе. Затем из начала вектора  и конца вектора
и конца вектора 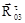 проводим прямые, параллельные соответственно звеньям 2 и 3. Точка пересечения этих прямых определит длины векторов
проводим прямые, параллельные соответственно звеньям 2 и 3. Точка пересечения этих прямых определит длины векторов  , которую определяем из графического решения уравнения
, которую определяем из графического решения уравнения (1.39)
(1.39)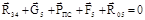 , (1.40)
, (1.40) . (1.41)
. (1.41)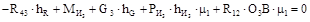 , (1.42)
, (1.42)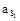 = 0, так как
= 0, так как 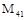 – главный момент от сил инерции, Н·м,
– главный момент от сил инерции, Н·м,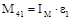 ,(1.43)
,(1.43)
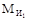 . Величина уравновешивающей силы определяется из уравнения моментов сил, действующих на кривошип АВ, относительно шарнира А. Условие равновесия кривошипа под действием заданной системы сил определяется векторным уравнением
. Величина уравновешивающей силы определяется из уравнения моментов сил, действующих на кривошип АВ, относительно шарнира А. Условие равновесия кривошипа под действием заданной системы сил определяется векторным уравнением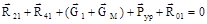 . (1.45)
. (1.45)


