Решение. Здесь требуется найти разность потенциалов между точками a и b, которую измеряет вольтметр, подключенный к этим точкам
Здесь требуется найти разность потенциалов между точками a и b, которую измеряет вольтметр, подключенный к этим точкам. Если бы вольтметр обладал бесконечно большим сопротивлением и тока через него не было, то эта задача была бы решена с помощью закона Ома для участка неоднородной цепи. Однако в данном случае сопротивление Таким образом, здесь имеется разветвленная цепь, по трем участкам которой текут, вообще говоря, разные токи: Искомая разность потенциалов по закону Ома (15.14) равна
Чтобы определить силу тока
Для составления остальных двух независимых уравнений воспользуемся вторым правилом Кирхгофа. Предварительно выбрав направление обхода замкнутых контуров, например по часовой стрелке, и учитывая правило знаков (см. раздел 15.5.4), получим соответственно для контуров
Решив систему трех уравнений (15.27), (15.28), (15.29) с тремя неизвестными
Подставив это значение
Знак «—» в ответе означает, что
|

 одного порядка с
одного порядка с  и
и 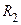 , поэтому пренебречь током
, поэтому пренебречь током  в цепи вольтметра нельзя.
в цепи вольтметра нельзя. (рис. 15.4). Задачу можно решить, используя правила Кирхгофа для разветвленных цепей.
(рис. 15.4). Задачу можно решить, используя правила Кирхгофа для разветвленных цепей. (15.26)
(15.26) (15.27)
(15.27) и
и  :
: ,(15.28)
,(15.28) (15.29)
(15.29) относительно тока
относительно тока  (15.30)
(15.30)

 >
>  и в действительности ток в цепи вольтметра имеет направление, противоположное тому, что мы предположили, т. е. от точки b к точке а.
и в действительности ток в цепи вольтметра имеет направление, противоположное тому, что мы предположили, т. е. от точки b к точке а.


