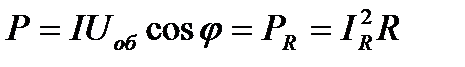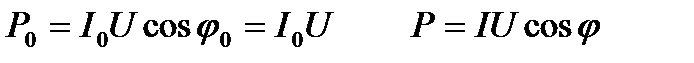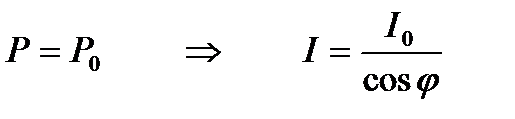Разветвленная цепь переменного тока
Решение 1. Резистор и конденсатор соединены последовательно, значит, токи в этих элементах цепи одинаковые 2. Построение векторной диаграммы начнем с тока
По условию 3. На индуктивной нагрузке ток отстает по фазе от напряжения на
4. Ток в неразветвленной части цепи
5. Из векторной диаграммы нетрудно видеть, что 6. Составляющие тока
7. Очевидно, что ток в неразветвленной части цепи равен
10. Опять о мощности в цепи переменного тока Как мы только что показали, конденсатор и катушка не потребляют энергию от источника за период. Остается предположить, что преобразование электрической энергии безвозвратно в тепловую энергию происходит исключительно за счет наличия в цепи активной нагрузки. Рассмотрим знакомый пример – последовательное соединение R,L, и С.
Мощность, потребляемая цепью, равна:
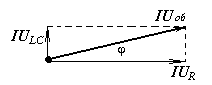
Из треугольника напряжений нетрудно видеть, что
Что и требовалось доказать.
Кстати, тогда для расчета мощности, потребляемой всей цепью не обязательно находить общий ток, общее напряжение и сдвиг фаз между ними. Достаточно воспользоваться законом Джоуля-Ленца для каждого резистора, входящего в состав цепи:
Введем еще ряд важных понятий.
Вводят следующие обозначения
Полную мощность S иначе называют кажущейся, т.е. такой, которую мог бы дать источник, если бы не было сдвига по фазе между током и напряжением. Единицы измерения полной мощности [S] = [В×А]. Реактивная мощность Q – это та энергия, которой в течение периода цепь обменивается с источником. Ее измеряют в Вольт-Амперах реактивных (Вар). Только активная мощность Р соответствует электрической энергии, используемой для преобразования в тепло, для получения механической работы и т.д.
Низкие значения cosj порождают значительные дополнительные потери на нагревание подводящих проводов, обмоток генератора. Покажем это. Пусть одинаковые мощности передаются от одинаковых генераторов двум нагрузкам с cosj0=1 и cosj<1.
Мощность, расходуемая на нагревание проводов, по закону Джоуля -Ленца будет равна
|

 Определите силу тока в неразветвленной части цепи и напряжение на клеммах источника, если
Определите силу тока в неразветвленной части цепи и напряжение на клеммах источника, если  , ток через катушку равен 10 А, ток в ветви, содержащей конденсатор и резистор – 14,1 А.
, ток через катушку равен 10 А, ток в ветви, содержащей конденсатор и резистор – 14,1 А.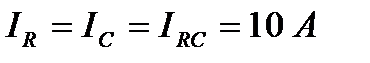 . Катушка включена параллельно ветви RC, следовательно, одинаковы напряжения
. Катушка включена параллельно ветви RC, следовательно, одинаковы напряжения 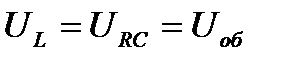 .
. 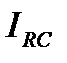 - расположим его горизонтально. Напряжение на активной нагрузке
- расположим его горизонтально. Напряжение на активной нагрузке 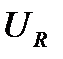 совпадает с током по фазе, следовательно, вектор
совпадает с током по фазе, следовательно, вектор 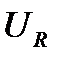 на диаграмме будет параллелен вектору тока
на диаграмме будет параллелен вектору тока 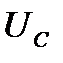 отстает от тока по фазе на
отстает от тока по фазе на  .
. 
 . При последовательном соединении напряжения на участках с одинаковым сопротивлением тоже равны
. При последовательном соединении напряжения на участках с одинаковым сопротивлением тоже равны 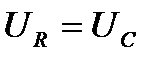 . На диаграмме вектора
. На диаграмме вектора 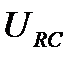 равен
равен  .
.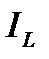 на диаграмме длиннее вектора
на диаграмме длиннее вектора 
 складывается из токов в ветвях
складывается из токов в ветвях  и
и 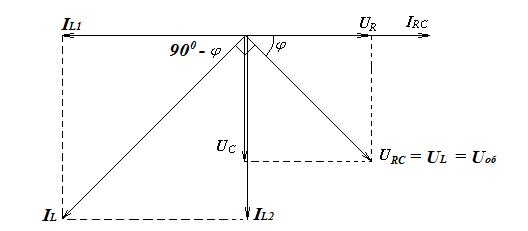
 .
.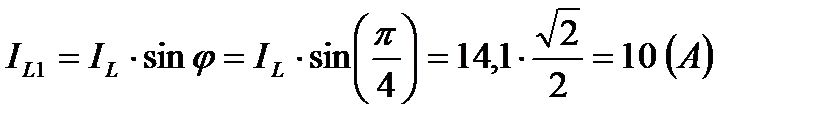 и
и .
.
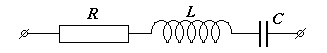
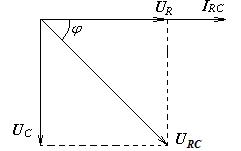
 Векторная диаграмма для такой цепи нам уже знакома:
Векторная диаграмма для такой цепи нам уже знакома: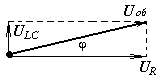



 Важно, что наш вывод верен для любого вида соединения. Преобразование электрической энергии в цепи переменного тока в тепловую энергию происходит только на активной нагрузке!
Важно, что наш вывод верен для любого вида соединения. Преобразование электрической энергии в цепи переменного тока в тепловую энергию происходит только на активной нагрузке!