Определение удельных приростов потерь
Как известно технические потери активной мощности в сети p имеют две составляющие: условно постоянную и переменную При распределении мощности необходимо учитывать нагрузочные потери
При решении задачи оптимального распределения активной мощности будем считать, что потери p зависят только от P:
В простейшем случае (рис.1.29) зависящая от мощности Рi часть потерь
и удельный прирост потерь равен
Оценим возможную величину прироста потерь при RS = 10 Ом, UH = 110 кВ, Pi = 50 МВт. В этом случае прирост составляет
Значение удельного прироста позволяет оценивать изменение потерь в сети при изменении узловой мощности
В сложных системах
Здесь Коэффициент потокораспределения Для определения a вводят балансирующий узел и выбирают положительные направления ветвей. Все a определяются расчетом токов в R-схеме при фиксированном токе Ii = 1 только в одном i-м узле и отсутствии токов в остальных узлах. На рис.1.30 показана расчетная R-схема сети и подготовленные для определения asi три схемы
Рис. 1.30 Результаты расчета приведены в таблице.
Матрицу коэффициентов токораспределения можно получить по формуле A = R -1 M T Y -1, где R – матрица сопротивлений ветвей, M – матрица соединений узлы-ветви, Y – матрица узловых проводимостей.
Обычно нагрузки Pa, Pb, … известны, поэтому нагрузочный поток в каждой ветви можно найти путем суммирования
где P1, P2, … – нагрузки ЭС, являющиеся неизвестными при распределении. Потери в сети после преобразований можно записать в виде:
Здесь
В матричной записи получена общая формула потерь:
где
Общая формула потерь позволяет приближенно учитывать потери в сети при оптимизации. Аналогично могут быть найдены потери от реактивной мощности источников
где
|

 . При этом
. При этом  зависит от уровня напряжения, а
зависит от уровня напряжения, а 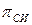 зависит от загрузки линий.
зависит от загрузки линий.
 .
. активной мощности в сети
активной мощности в сети
 .
. .
. .
. определяют в предположении линейной зависимости потоков в ветвях
определяют в предположении линейной зависимости потоков в ветвях 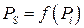 от мощности узлов, т.е.
от мощности узлов, т.е. .
. – мощности нагрузок,
– мощности нагрузок,  – коэффициенты.
– коэффициенты. показывают, какая доля мощности i-го узла течет по ветви s.
показывают, какая доля мощности i-го узла течет по ветви s.
 . Полный поток в ветви будет зависеть от мощностей ЭС
. Полный поток в ветви будет зависеть от мощностей ЭС ,
,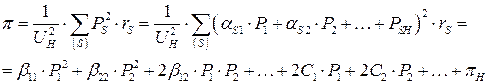
 ,
,  ,
,  ,
, .
. ,
, – вектор неизвестных мощностей ЭС,
– вектор неизвестных мощностей ЭС, и
и  – матрицы коэффициентов.
– матрицы коэффициентов. ,
, и
и  определяются реактивными нагрузками в узлах, при этом
определяются реактивными нагрузками в узлах, при этом 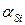 не меняются.
не меняются.


