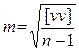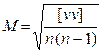Равноточные измерения
Измерения, выполняемые в одинаковых условиях по одной и той же методике, называют равноточными. 6.2.1 Простая арифметическая середина. Пусть в результате равноточных измерений величины, истинное значение которой L, получены ее значения l1, l2, …, ln. Тогда истинные погрешности измерений d1 = l1 – L, d2 = l2 – L, …, dn = ln – L. Сложив эти равенства, получим [d] = [ l ] – nL. Отсюда
где Поскольку при n®¥ При конечном числе измерений арифметическая середина является наиболее точным значением измеряемой величины, а значение (X – L) называется случайной погрешностью простой арифметической середины. 6.2.2 Средняя квадратическая, относительная и предельная погрешности. При выборе критерия оценки точности наблюдений следует иметь ввиду, что на практике результат считается одинаково ошибочным, будет ли он больше или меньше истинного значения на некоторую величину. Поэтому за меру случайных погрешностей может быть принят критерий, который не зависел бы от знаков отдельных погрешностей и чутко отражал наличие в данном ряду измерений сравнительно крупных погрешностей. Таким требованиям удовлетворяет средняя квадратическая погрешность, определяемая по формуле Гаусса:
Отношение абсолютной погрешности (истинной или средней квадратической) к значению измеряемой величины называется относительной погрешностью. Относительной погрешностью характеризуют, как правило, линейные измерения. Она выражается правильной дробью, числитель которой равен единице:
Предельной погрешностью называется такое значение случайной погрешности, появление которого при данных условиях измерений маловероятно. Установлено, что случайная погрешность измерения может превысить среднюю квадратическую примерно в 32 случаях из 100, удвоенную среднюю квадратическую погрешность – в 4 случаях из 100, утроенную – в 3 случаях из 1000. Поэтому в топографо-геодезических работах за предельную допустимую величину погрешности обычно принимают удвоенную среднюю квадратическую погрешность. 6.2.3 Средняя квадратическая погрешность функции измеренных величин. Пусть дана функция общего вида y = f (x1, x2, …, xn), аргументы которой х1, х2, …, хп независимо измерены со средними квадратическими погрешностями т1, т2, … тп. В теории погрешностей измерений доказывается, что средняя квадратическая погрешность функции определяется из выражения:
где Например: y = x × z, где величина х определена с погрешностью тх, а z – с погрешностью mz. Тогда имеем:
Тогда My2 = x2×mz2 + z2×mx2 6.2.4 Средняя квадратическая погрешность простой арифметической середины. Представим формулу простой арифметической середины в виде:
Как видно, правая часть выражения представляет собой линейную функцию независимо измеренных аргументов l1, l2, …, ln. Тогда можно записать:
Поскольку величины l1, l2, …, ln измерены с одинаковой точностью, т.е. т1 = т2 = … = т, то выражение примет вид:
6.2.5 Средняя квадратическая погрешность измеренных величин по отклонениям их от простой арифметической середины. В большинстве случаев истинное значение L измеряемой величины неизвестно, поэтому для определения средней квадратической погрешности измерения невозможно использовать формулу Пусть имеем п измеренных значений величины l1, l2, …, ln, арифметическая середина которой v1 = l1 – X; v2 = l2 – X;; vn = ln – X. Сложив эти равенства, получим [v] = [l] – nX. Но nX = [l], следовательно [v] = 0, т.е. сумма уклонений отдельных результатов измерений от простой арифметической середины равна нулю. Зная уклонения v, можно вычислить среднюю квадратическую погрешность одного измерения по формуле Бесселя:
где [vv] – сумма квадратов уклонений измеренных значений величины от ее арифметической середины. Средняя квадратическая погрешность арифметической середины с учетом этого запишется как
|

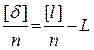
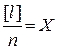 - среднее арифметическое или арифметическая середина.
- среднее арифметическое или арифметическая середина.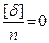 , следовательно
, следовательно 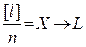 , т.е. арифметическая середина из результатов измерений l1, l2, …, ln при неограниченном увеличении n стремится к истинному значению измеряемой величины L.
, т.е. арифметическая середина из результатов измерений l1, l2, …, ln при неограниченном увеличении n стремится к истинному значению измеряемой величины L.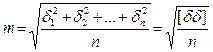


 - частные производные данной функции, вычисленные для соответствующих значений аргументов.
- частные производные данной функции, вычисленные для соответствующих значений аргументов.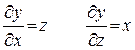
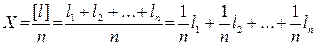
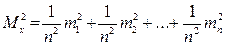
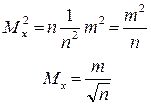
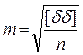 . В таких случаях оценку точности измерений производят по уклонениям v отдельных измерений от простой арифметической середины.
. В таких случаях оценку точности измерений производят по уклонениям v отдельных измерений от простой арифметической середины.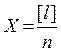 . Тогда уклонения измеренных значений от арифметической середины будут
. Тогда уклонения измеренных значений от арифметической середины будут