Плоская электромагнитная волна. Свойства электромагнитных волн.
Обратимся теперь к тем уравнениям Максвелла, которые связывают электрические и магнитные поля. Это две теоремы о циркуляции [см. (12.4) и (12.6) ]:
Выберем в пространстве небольшой прямоугольный контур со сторонами dy, dz, параллельными осям y и z (рис. 13.2.). Запишем первое уравнение системы (13.4) для этого контура.
Рис. 13.2. Вспомним, что левая часть этого уравнения — циркуляция вектора напряженности магнитного поля по выбранному контуру:
а правая — это ток проводимости и поток вектора
Приравняв два последних результата, получим
Выбрав два других контура с площадями dxdz и dxdy, вновь для них запишем первое уравнение системы (13.4). В итоге это уравнение можно будет представить следующими тремя уравнениями:
Поступив точно также со вторым уравнением системы (13.4), заменим его следующей тройкой дифференциальных уравнений:
Уравнения (13.5) и (13.6) — уравнения Максвелла в дифференциальной форме. Теперь конкретизируем задачу (правильнее было бы сказать — упростим). 1. Среда — однородный, изотропный диэлектрик. Это означает, что токи проводимости отсутствуют: jx = jy = jz = 0. 2. Будем рассматривать поля
Рис. 13.3. Для этого конкретного случая уравнения Максвелла (13.5) и (13.6) можно упростить и записать в таком виде
Эти уравнения означают, что изменяющееся во времени электрическое поле Dy рождает магнитное поле Hz, направленное вдоль оси z. Переменное магнитное поле By является источником электрического поля, меняющегося вдоль оси z. И так далее. В любом случае эти поля — Примем, для определенности, что электрическое поле направлено вдоль оси y (E = Ey, Ez = 0), а магнитное — вдоль оси z (H = Hz, Hy = 0). Тогда последняя система четырех уравнений упростится до двух:
Первое из этих уравнений продифференцируем по времени t, а второе — по координате x:
Сравнивая эти два уравнения, приходим к замечательному выводу:
Или еще понятнее:
Но теперь-то мы знаем, что это дифференциальное волновое уравнение. Таким образом, решая совместно уравнения Максвелла, мы пришли к выводу, что в однородной изотропной среде электрические (и магнитные!) поля распространяются в виде электромагнитной волны. Теперь известна и скорость этой волны:
Здесь Это значение — с = 3×108 м/с, как известно, великолепно подтверждается экспериментом. Подобное уравнение можно получить и для магнитной составляющей волны:
Решения этих волновых уравнений — (13.8) и (13.9) — хорошо известны:
Теперь найдем связь между мгновенными значениями напряженности электрического (Е) и магнитного (Н) полей. Для этого первое уравнение продифференцируем по t, а второе — по x:
Эти уравнения подставим в первое уравнение системы (13.7):
Проинтегрировав это равенство, получим
Поскольку речь идет о переменных полях, постоянную интегрирования можно положить равной нулю: С = 0. Тогда последнее уравнение можно будет представить так:
или
Этот результат означает, что напряженности электрического (Е) и магнитного (Н) полей в электромагнитной волне пропорциональны друг другу и меняются, следовательно, синфазно. Подводя итог, сформулируем еще раз основные свойства электромагнитных волн. 1. Электромагнитные волны поперечны, то есть
2. Скорость распространения волны в однородной среде
Здесь 3. Электрическое и магнитное поле в волне меняются в фазе. Мгновенные значения Е и Н пропорциональны друг другу:
|

 ,
,  . (13.4)
. (13.4)
 ,
,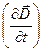 через площадку (dydz), ограниченную контуром 1-2-3-4-1:
через площадку (dydz), ограниченную контуром 1-2-3-4-1: .
. .
. (13.5)
(13.5) (13.6)
(13.6) и
и  ,зависящие только от одной координаты x и времени t. Это одномерная задача (рис. 13.3.).
,зависящие только от одной координаты x и времени t. Это одномерная задача (рис. 13.3.).

 и
и  (13.7)
(13.7)

 . (13.8)
. (13.8)
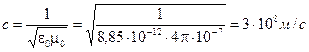 — скорость электромагнитной волны в вакууме (e = 1 и m = 1).
— скорость электромагнитной волны в вакууме (e = 1 и m = 1). (13.9)
(13.9)




 . (13.10)
. (13.10)

 — скорость электромагнитной волны в вакууме (e = 1, m = 1), e0 и m0 — диэлектрическая и магнитная проницаемости среды.
— скорость электромагнитной волны в вакууме (e = 1, m = 1), e0 и m0 — диэлектрическая и магнитная проницаемости среды.



