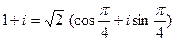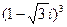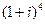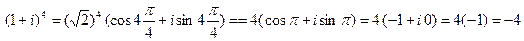Комплексное число  можно представить в виде упорядоченной пары
можно представить в виде упорядоченной пары  -радиус- вектор на комплексной плоскости с началом в начале координат и с концом в точке
-радиус- вектор на комплексной плоскости с началом в начале координат и с концом в точке  . При этом радиус-вектор или комплексное число
. При этом радиус-вектор или комплексное число  характеризуется модулем или длиной вектора
характеризуется модулем или длиной вектора  =
= 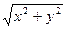 , с углом наклона
, с углом наклона 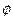 к оси абсцисс. Будем называть
к оси абсцисс. Будем называть 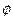 главным значением аргумента или аргументом, если
главным значением аргумента или аргументом, если 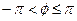 . Обозначается
. Обозначается  .
.
При этом 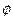 положителен, если он отсчитывается от положительного направления оси абсцисс против часовой стрелки, и отрицателен, если наоборот. Ясно, что
положителен, если он отсчитывается от положительного направления оси абсцисс против часовой стрелки, и отрицателен, если наоборот. Ясно, что  . Отсюда получаем тригонометрическую форму комплексного числа
. Отсюда получаем тригонометрическую форму комплексного числа  :
:
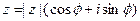
Используя разложение функций  и
и  в ряды Тейлора, можно показать, что
в ряды Тейлора, можно показать, что
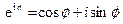 (формула Эйлера)
(формула Эйлера)
Если заданы 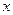 и
и  , то аргумент
, то аргумент 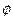 находится следующим образом:
находится следующим образом:
Точка z лежит в первой четверти комплексной плоскости,  . Тогда
. Тогда  . Точка z лежит во второй четверти комплексной плоскости,
. Точка z лежит во второй четверти комплексной плоскости,  . Тогда
. Тогда  . Точка z лежит в третьей четверти комплексной плоскости,
. Точка z лежит в третьей четверти комплексной плоскости, 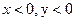 . Тогда
. Тогда  . Точка z лежит в четвертой четверти комплексной плоскости,
. Точка z лежит в четвертой четверти комплексной плоскости,  . Тогда
. Тогда  .
.
Рассмотрим частные случаи:
Если  , точка
, точка  лежит на оси
лежит на оси  справа от начала координат, тогда
справа от начала координат, тогда 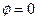 . Если
. Если  , точка
, точка  лежит на оси
лежит на оси 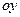 выше начала координат, тогда
выше начала координат, тогда  . Если
. Если  , точка
, точка  лежит на оси
лежит на оси  слева от начала координат, тогда
слева от начала координат, тогда  . Если
. Если 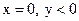 , точка
, точка  лежит на оси
лежит на оси 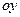 ниже начала координат, тогда
ниже начала координат, тогда  .
.
Если,  , точка
, точка  лежит в четвертой четверти,
лежит в четвертой четверти,  . Если
. Если  , точка
, точка  лежит в первой четверти,
лежит в первой четверти,  . Если
. Если  , точка
, точка  лежит во второй четверти,
лежит во второй четверти,  . Если
. Если  , точка
, точка  лежит в четвертой четверти,
лежит в четвертой четверти,  . Если
. Если  , точка
, точка  лежит в третьей четверти,
лежит в третьей четверти,  .
.
Можно показать, что, если  ,
,  , то
, то
 ,
,
в частности, если умножим число  само на себя
само на себя  раз, получим формулу Муавра
раз, получим формулу Муавра
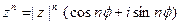
Пример 10. Записать в тригонометрической форме числа
1)  ; 2)
; 2) 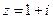
Решение. 1)  . Отсюда
. Отсюда 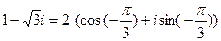
2)  . Отсюда
. Отсюда 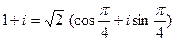
В следующих двух примерах применим формулу Муавра.
Пример 11. Найти 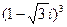
Решение. 
Пример 12. Найти 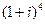
Решение. Имеем
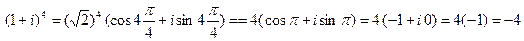

 можно представить в виде упорядоченной пары
можно представить в виде упорядоченной пары  -радиус- вектор на комплексной плоскости с началом в начале координат и с концом в точке
-радиус- вектор на комплексной плоскости с началом в начале координат и с концом в точке  =
= 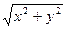 , с углом наклона
, с углом наклона 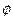 к оси абсцисс. Будем называть
к оси абсцисс. Будем называть 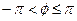 . Обозначается
. Обозначается  .
. . Отсюда получаем тригонометрическую форму комплексного числа
. Отсюда получаем тригонометрическую форму комплексного числа 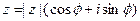
 и
и  в ряды Тейлора, можно показать, что
в ряды Тейлора, можно показать, что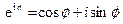 (формула Эйлера)
(формула Эйлера)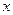 и
и  , то аргумент
, то аргумент  . Тогда
. Тогда  . Точка z лежит во второй четверти комплексной плоскости,
. Точка z лежит во второй четверти комплексной плоскости,  . Тогда
. Тогда  . Точка z лежит в третьей четверти комплексной плоскости,
. Точка z лежит в третьей четверти комплексной плоскости, 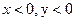 . Тогда
. Тогда  . Точка z лежит в четвертой четверти комплексной плоскости,
. Точка z лежит в четвертой четверти комплексной плоскости,  . Тогда
. Тогда  , точка
, точка  справа от начала координат, тогда
справа от начала координат, тогда 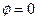 . Если
. Если 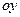 выше начала координат, тогда
выше начала координат, тогда  . Если
. Если  , точка
, точка  . Если
. Если 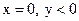 , точка
, точка  .
. , точка
, точка  . Если
. Если  , точка
, точка  . Если
. Если  , точка
, точка  . Если
. Если  , точка
, точка  . Если
. Если  , точка
, точка  .
. ,
,  , то
, то ,
, само на себя
само на себя  раз, получим формулу Муавра
раз, получим формулу Муавра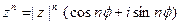
 ; 2)
; 2) 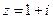
 . Отсюда
. Отсюда 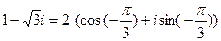
 . Отсюда
. Отсюда