Интегрирование подведением под знак дифференциала.
Для использования метода запишем таблицу дифференциалов, которая легко получается из таблицы производных и таблицы интегралов. В первом случае применяем формулы для дифференциалов функции, записанных в обратном порядке, во втором – путем взятия знака дифференциала от обеих частей равенства. Таблица дифференциалов. 1. 2. 3. 4. 5. 6. 7. Примечание. Формулы для дифференциалов функции Поэтому таблица дифференциалов будет иметь место, если вместо x подставить u(t). C помощью формулы для дифференциала функции записанной в обратном порядке некоторые интегралы
Указанное преобразование называется «Подведение под знак дифференциала». Примеры. 1) = 2) 3) 4) 5) = 2. Метод подстановки. Иногда удается подобрать в качестве новой переменной такую дифференцируемую функцию
Указанный прием вычисления интеграла
Примеры. 1)
2) тогда dt=d(ax+b)=(ax+b
3) Подстановка
4)
5)
|

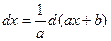 8.
8. 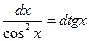
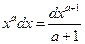 9.
9. 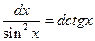
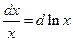 10.
10. 
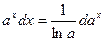 11
11 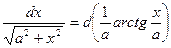
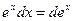 12.
12. 

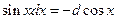 13.
13. 
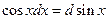
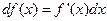 не меняются от того является ли x независимой переменной или есть некоторая функция u(t) другой независимой переменной t. (свойства инвариантности формы первого дифференциала)
не меняются от того является ли x независимой переменной или есть некоторая функция u(t) другой независимой переменной t. (свойства инвариантности формы первого дифференциала)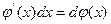
 могут быть сведены к виду
могут быть сведены к виду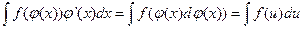 , которые легко сводятся к табличным. Здесь
, которые легко сводятся к табличным. Здесь 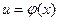 .
.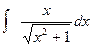 =
= 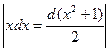 = =
= =  =
= =
= 
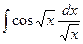 =
=  =
= 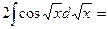
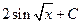 .
. =
= 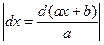 =
=  =
= 
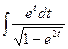 =
= 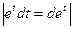 =
= 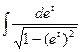 =arcsin(
=arcsin( )+ C
)+ C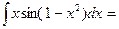
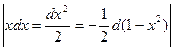 =
=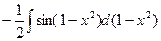 =
= 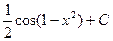
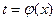 , что имеет место равенство f(x)dx = q(
, что имеет место равенство f(x)dx = q(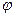 (x))
(x)) 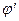 (x)dx, причем интеграл
(x)dx, причем интеграл 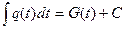 легко вычисляется. Таким образом:
легко вычисляется. Таким образом: =
= 
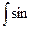 (6x-5)dx. Подстановка
(6x-5)dx. Подстановка 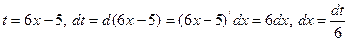
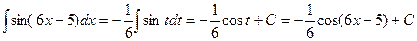
 ; подстановка t=ax+b,
; подстановка t=ax+b, dx=adx, dx=
dx=adx, dx= 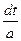 ,
, =
= 
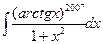 .
.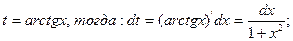
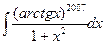 =
= 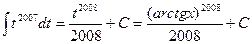
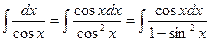 ; подстановка
; подстановка
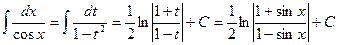
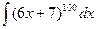 ; подстановка
; подстановка 




