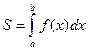Пусть  определена на сегменте
определена на сегменте 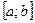
Определение. Разбиение  сегмента
сегмента  задано, если заданы точки
задано, если заданы точки  такие, что
такие, что 
Обозначим через  длину частичного сегмента
длину частичного сегмента  Максимальную из этих длин обозначим
Максимальную из этих длин обозначим  которую назовём диаметром разбиения
которую назовём диаметром разбиения  В частичном сегменте выберем произвольную точку
В частичном сегменте выберем произвольную точку 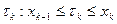
Определение. Выражение  называется интегральной суммой и обозначается
называется интегральной суммой и обозначается 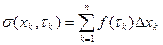
Определение. Число  называется пределом интегральных сумм
называется пределом интегральных сумм  при стремлении диаметра разбиений
при стремлении диаметра разбиений  к нулю, если для любого
к нулю, если для любого  существуют такие
существуют такие  что из условия
что из условия  при любом выборе промежуточных точек
при любом выборе промежуточных точек 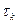 следует неравенство
следует неравенство  . При этом пишут
. При этом пишут 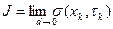
Определение. Функция  называется интегрируемой на сегменте
называется интегрируемой на сегменте 
 если для этой функции существует предел
если для этой функции существует предел  её интегральных сумм
её интегральных сумм  при стремлении диаметра
при стремлении диаметра  разбиений
разбиений  к нулю.
к нулю.
Число  называется определённым интегралом от функции
называется определённым интегралом от функции  в пределах от а до в и обозначается
в пределах от а до в и обозначается 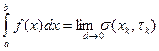
Числа  и
и  – пределы интегрирования (
– пределы интегрирования ( – нижний предел,
– нижний предел,  – верхний предел).
– верхний предел).
Примечание. Переменную х под знаком определённого интеграла
можно заменить на любую другую переменную:  и т.д.
и т.д.
Теорема. Если функция  непрерывна на сегменте
непрерывна на сегменте  , то она интегрируема на нём.
, то она интегрируема на нём.
Пример. 1. Путь S, пройденный точкой за время  со скоростью
со скоростью  , есть S=
, есть S=  .
.
2. Работа А, совершаемая над материальной точкой переменной силой f(x), есть  .
.
3. Площадь криволинейной трапеции, ограниченной сверху графиком неотрицательной непрерывной функции  ,
,
снизу – осью Ох, с боков – прямыми  равна
равна
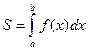

 определена на сегменте
определена на сегменте 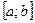
 сегмента
сегмента  задано, если заданы точки
задано, если заданы точки  такие, что
такие, что 
 длину частичного сегмента
длину частичного сегмента  Максимальную из этих длин обозначим
Максимальную из этих длин обозначим  которую назовём диаметром разбиения
которую назовём диаметром разбиения  В частичном сегменте выберем произвольную точку
В частичном сегменте выберем произвольную точку 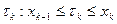
 называется интегральной суммой и обозначается
называется интегральной суммой и обозначается 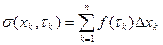
 называется пределом интегральных сумм
называется пределом интегральных сумм  при стремлении диаметра разбиений
при стремлении диаметра разбиений  существуют такие
существуют такие  что из условия
что из условия  при любом выборе промежуточных точек
при любом выборе промежуточных точек 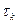 следует неравенство
следует неравенство  . При этом пишут
. При этом пишут 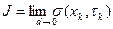

 если для этой функции существует предел
если для этой функции существует предел  при стремлении диаметра
при стремлении диаметра  разбиений
разбиений 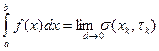
 и
и  – пределы интегрирования (
– пределы интегрирования ( и т.д.
и т.д. , то она интегрируема на нём.
, то она интегрируема на нём. со скоростью
со скоростью  , есть S=
, есть S=  .
. .
. ,
, равна
равна