|
| Наименование операции
| Формулы
|
|
| Сложение и вычитание в алгебраической форме
| 
|
|
| Сложение и вычитание сопряженных чисел
| 
|
|
| Умножение в алгебраической форме
| 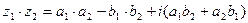
|
|
| Умножение сопряженных чисел
| 
|
|
| Деление в алгебраической форме
| 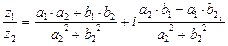
|
|
| Умножение в показательной форме
| 
|
|
| Умножение в тригонометрической форме
| 
|
|
| Деление в показательной форме
| 
|
|
| Деление в тригонометрической форме
| 
|
|
| Возведение в целую степень в показательной и тригонометрической формах
| 
|
|
| Корень целой степени
| 
|
|
| Формула Эйлера
|  
|
|
| Формула Муавра
| 
|
Обозначение:

Комплексным числом  называется величина
называется величина  , где х и у действительные числа, называемые действительной и мнимой частями числа
, где х и у действительные числа, называемые действительной и мнимой частями числа  ,
,  - мнимая единица,
- мнимая единица,  . Таким образом,
. Таким образом, 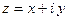
Суммой комплексных чисел  и
и  наз.к.ч.
наз.к.ч.  , равное
, равное


Произведением действительного числа  на комплексное число
на комплексное число  наз.величина
наз.величина  , равная
, равная

Разность комплексных чисел  и
и  равна
равна

Пример 1. 
Произведение комплексных чисел 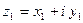 и
и  находится по правилу
находится по правилу
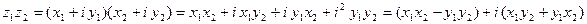 .
.
Таким образом,  .
.
Пример 2. 
Пример 3. 
Пример 4. 
Пример 5. 
Пример 6. 
Число  называется сопряженным к комплексному числу
называется сопряженным к комплексному числу 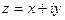 .
.
Имеем 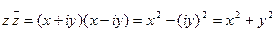
Частным  и
и 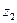 называется число
называется число  , для которого
, для которого  . Частное обозначается
. Частное обозначается
 . Вычисляется по правилу:
. Вычисляется по правилу: 
Таким образом, 
Пример 7. 
Пример 8. 
Пример 9. 



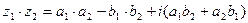

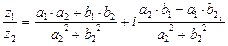










 называется величина
называется величина  , где х и у действительные числа, называемые действительной и мнимой частями числа
, где х и у действительные числа, называемые действительной и мнимой частями числа  - мнимая единица,
- мнимая единица,  . Таким образом,
. Таким образом, 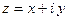
 и
и  наз.к.ч.
наз.к.ч.  , равное
, равное

 на комплексное число
на комплексное число  , равная
, равная
 равна
равна

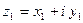 и
и 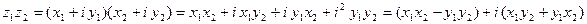 .
. .
.




 называется сопряженным к комплексному числу
называется сопряженным к комплексному числу 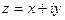 .
.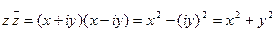
 и
и 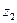 называется число
называется число  . Частное обозначается
. Частное обозначается . Вычисляется по правилу:
. Вычисляется по правилу: 







