Определение. Преобразованием Лапласа функции  называется интеграл
называется интеграл  и обозначается
и обозначается 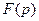 . Таким образом,
. Таким образом,
 , где
, где
 - действительная переменная,
- действительная переменная,  - комплексная переменная. При этом функция
- комплексная переменная. При этом функция  называется оригиналом,
называется оригиналом, 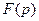 -изображением.
-изображением.
Условия, которым должен удовлетворять оригинал  :
:
1) 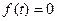 при
при 
2) Не иметь знаменатель, который обращается в ноль. Например, функция  не может быть оригиналом.
не может быть оригиналом.
3) С возрастанием  модуль функции
модуль функции 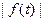 не может расти быстрее некоторой показательной функции, то есть,
не может расти быстрее некоторой показательной функции, то есть,  , где
, где  .
.
Например, функция  не может быть оригиналом, так как при любых числах
не может быть оригиналом, так как при любых числах  , данная функция растет быстрее чем функция
, данная функция растет быстрее чем функция 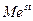 , то есть нарушается условие (3).
, то есть нарушается условие (3).
Свойство линейности изображения
Обозначим  .Пусть оригиналы
.Пусть оригиналы  и
и  имеют изображения
имеют изображения 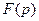 и
и  . Тогда
. Тогда 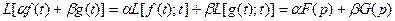 . Таким образом, изображением суммы
. Таким образом, изображением суммы 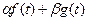 является
является  .
.
Пример 1. Найти изображение функции  .
.
Решение. Имеем 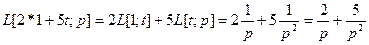 . Таким образом, изображением функции
. Таким образом, изображением функции  является
является  так, как изображением 1 согласно таблице является
так, как изображением 1 согласно таблице является  , а изображением
, а изображением  является
является  .
.
Пример 2. Найти изображение функции 3.
Решение. Имеем  . Таким образом, изображением функции
. Таким образом, изображением функции  является
является 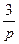 .
.
Пример 3. Какой оригинал соответствует изображению 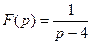 .
.
Решение. Согласно (4) таблицы изображений имеем при 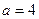 оригинал вида
оригинал вида

Пример 4. Найти изображение решения задачи Коши: 
Решение. Имеем  , где
, где

или  . Отсюда находим
. Отсюда находим  :
:  ,
,
 . Ответ:
. Ответ: 
Пример5. Записать в изображениях решение задачи Коши вида

Решение. Имеем

Далее  ,
,  . Отсюда
. Отсюда

Ответ

Таблица изображений
| Nпп
| Оригинал  
| Изображение 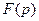
|
|
|
| 
|
|
| 
| 
|
|
| 
| 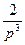
|
|
| 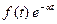
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 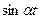
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 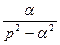
|
|
| 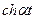
| 
|
|
| 
| 
|
|
| 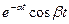
| 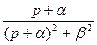
|
|
|  -производная -производная
|  , где , где 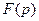 -изображение -изображение 
|
|
|  -вторая производная -вторая производная
|  , где , где 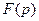 -изображение -изображение 
|
|
|  - третья производная - третья производная
| 
|
|
| 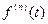 - -  -я производная -я производная
| 
|
|
| 
|  
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|

 называется интеграл
называется интеграл  и обозначается
и обозначается 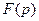 . Таким образом,
. Таким образом, , где
, где - действительная переменная,
- действительная переменная,  - комплексная переменная. При этом функция
- комплексная переменная. При этом функция 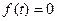 при
при 
 не может быть оригиналом.
не может быть оригиналом.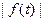 не может расти быстрее некоторой показательной функции, то есть,
не может расти быстрее некоторой показательной функции, то есть,  , где
, где  .
. не может быть оригиналом, так как при любых числах
не может быть оригиналом, так как при любых числах  , данная функция растет быстрее чем функция
, данная функция растет быстрее чем функция 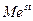 , то есть нарушается условие (3).
, то есть нарушается условие (3). .Пусть оригиналы
.Пусть оригиналы  имеют изображения
имеют изображения  . Тогда
. Тогда 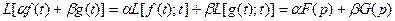 . Таким образом, изображением суммы
. Таким образом, изображением суммы 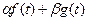 является
является  .
. .
.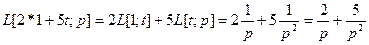 . Таким образом, изображением функции
. Таким образом, изображением функции  так, как изображением 1 согласно таблице является
так, как изображением 1 согласно таблице является  , а изображением
, а изображением  .
. . Таким образом, изображением функции
. Таким образом, изображением функции  является
является 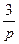 .
.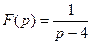 .
.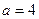 оригинал вида
оригинал вида

 , где
, где
 . Отсюда находим
. Отсюда находим  :
:  ,
, . Ответ:
. Ответ: 


 ,
,  . Отсюда
. Отсюда



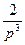
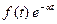







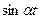









 -производная
-производная
 , где
, где  -вторая производная
-вторая производная
 , где
, где  - третья производная
- третья производная

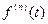 -
-  -я производная
-я производная












