Множество числовых отрезков { 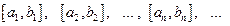 }
}
называется системой вложенных отрезков, если справедливы следующие неравенства:
 ,
,
то есть если 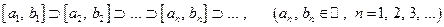

| Теорема о пересечении системы вложенных отрезков
|
| Всякая система вложенных отрезков имеет непустое пересечение
|
w Пусть имеем систему вложенных отрезков. Обозначим  - множество всех левых концов,
- множество всех левых концов,  - множество всех правых концов.
- множество всех правых концов.
Из неравенств, определяющих вложенные отрезки, следует, что 
 по свойству непрерывности множества
по свойству непрерывности множества  заключаем, что существует число
заключаем, что существует число  , такое что выполняется неравенство
, такое что выполняется неравенство  .
.
В частности, последнее неравенство выполняется при  , т.е.
, т.е. 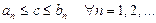
Следовательно, число с принадлежит всем отрезкам 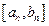 , поэтому это число принадлежит их пересечению. Таким образом доказано, что пересечение вложенных отрезков
, поэтому это число принадлежит их пересечению. Таким образом доказано, что пересечение вложенных отрезков  не является пустым. v
не является пустым. v
Можно сформулировать условие, при котором пересечение системы вложенных отрезков состоит лишь из единственной точки.
Длины  отрезков
отрезков  называются длинами отрезков, стремящимися к нулю, если для любого числа
называются длинами отрезков, стремящимися к нулю, если для любого числа 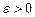 существует номер
существует номер  , такой что при всех
, такой что при всех  выполняется неравенство
выполняется неравенство 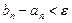 .
.
| Теорема о пересечении вложенных отрезков, длины которых стремятся к нулю
|
Для всякой системы вложенных отрезков  , длины которых стремятся к нулю, существует единственная точка , длины которых стремятся к нулю, существует единственная точка  , принадлежащая всем отрезкам данной системы. , принадлежащая всем отрезкам данной системы.
|
w По предыдущей теореме о пересечении вложенных отрезков имеем, что  . Предположим, что существуют две точки
. Предположим, что существуют две точки 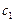 и
и  , принадлежащие пересечению всех отрезков:
, принадлежащие пересечению всех отрезков:  и
и  .
.
Тогда величина расстояния между числами 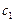 и
и  не превышает длины любого из этих отрезков:
не превышает длины любого из этих отрезков:  .
.
Но так как длины всех отрезков стремятся к нулю, то есть становятся меньше любого наперед заданного числа 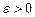 , то величина расстояния между числами
, то величина расстояния между числами 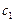 и
и  также меньше числа
также меньше числа  :
: 
 .
.
Здесь  - это произвольное, сколь угодно малое число, поэтому неравенство
- это произвольное, сколь угодно малое число, поэтому неравенство  возможно только в случае
возможно только в случае  .
.
Таким образом доказано, что существует единственное число с, принадлежащее всем вложенным отрезкам, длины которых стремятся к нулю: 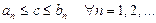 v
v
Замечания (к принципу вложенных отрезков)
1. Для интервалов и полуинтервалов множества  аналог принципа вложенных отрезков не имеет места.
аналог принципа вложенных отрезков не имеет места.
Например,  , то есть система вложенных интервалов или полуинтервалов может иметь пустое пересечение
, то есть система вложенных интервалов или полуинтервалов может иметь пустое пересечение
2. Для множества одних только рациональных чисел утверждения принципа вложенных отрезков не являются верными. При этом под отрезком понимается пересечение обычного отрезка, концы которого являются рациональными числами, с множеством рациональных чисел, т.е.
 .
.
Например, рассмотрим 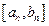 , где
, где  - десятичные приближения соответственно с недостатком и избытком числа
- десятичные приближения соответственно с недостатком и избытком числа  , имеющие по
, имеющие по  знаков после запятой:
знаков после запятой:
 ,
,  ,
, 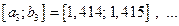
Тогда  , так как
, так как  .
.

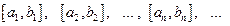 }
} ,
,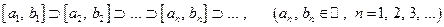

 - множество всех левых концов,
- множество всех левых концов,  - множество всех правых концов.
- множество всех правых концов.
 по свойству непрерывности множества
по свойству непрерывности множества  заключаем, что существует число
заключаем, что существует число  , такое что выполняется неравенство
, такое что выполняется неравенство  .
. , т.е.
, т.е. 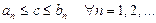
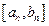 , поэтому это число принадлежит их пересечению. Таким образом доказано, что пересечение вложенных отрезков
, поэтому это число принадлежит их пересечению. Таким образом доказано, что пересечение вложенных отрезков  не является пустым. v
не является пустым. v отрезков
отрезков  называются длинами отрезков, стремящимися к нулю, если для любого числа
называются длинами отрезков, стремящимися к нулю, если для любого числа 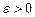 существует номер
существует номер  , такой что при всех
, такой что при всех  выполняется неравенство
выполняется неравенство 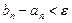 .
. , длины которых стремятся к нулю, существует единственная точка
, длины которых стремятся к нулю, существует единственная точка  , принадлежащая всем отрезкам данной системы.
, принадлежащая всем отрезкам данной системы.
 . Предположим, что существуют две точки
. Предположим, что существуют две точки 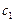 и
и  , принадлежащие пересечению всех отрезков:
, принадлежащие пересечению всех отрезков:  и
и  .
. .
. :
: 
 .
. возможно только в случае
возможно только в случае  .
. , то есть система вложенных интервалов или полуинтервалов может иметь пустое пересечение
, то есть система вложенных интервалов или полуинтервалов может иметь пустое пересечение .
. - десятичные приближения соответственно с недостатком и избытком числа
- десятичные приближения соответственно с недостатком и избытком числа  , имеющие по
, имеющие по  знаков после запятой:
знаков после запятой: ,
,  ,
, 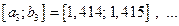
 , так как
, так как  .
.


