Аксиоматическое определение множества действительных чисел
Множеством действительных чисел
I. Для 1) a + b = b + a – свойство коммутативности операции сложения; 2) a + b + c =(a + b) + c — свойство ассоциативности операции сложения; 3) $ число ноль 4) для 5) число a + (–b) = a – b называется разностью чисел a и b.
II. Для 1) a·b = b·a – свойство коммутативности операции умножения; 2) a·b·c =(a·b) ·c – свойство ассоциативности операции умножения; 3) $ число единица 4) для 5) число
III. Имеет место свойство дистрибутивности произведения относительно суммы: (a + b) ·c = a·c + b·c для
IV. Упорядоченность множества действительных чисел Для a < b или a = b или a > b. При этом выполняются условия: 1) если a < b и b < c, то a < c — транзитивность; 2) если a < b, то a + c < b + c для 3) если a < b и c > 0, то a · c < b · c. Как следствие этих условий получается свойство плотности множества действительных чисел для w Отношения порядка называются неравенствами или сравнениями действительных чисел. Нестрогие неравенства:
V. Непрерывность множества действительных чисел Для любых непустых множеств
Рис. 12 Перечисленные свойства I-V определяют множество Геометрическая интерпретация множества Геометрическая интерпретация множества
Рис. 13 Смысл этой интерпретации состоит в том, что любому числу
|

 называется множество, содержащее более одного элемента и удовлетворяющее следующим свойствам I‑V.
называется множество, содержащее более одного элемента и удовлетворяющее следующим свойствам I‑V. определено единственное число a + b, называемое суммой двух действительных чисел, так что выполняются условия:
определено единственное число a + b, называемое суммой двух действительных чисел, так что выполняются условия: такое, что a + 0= a для
такое, что a + 0= a для 

 такое, что a +(–a)= 0;
такое, что a +(–a)= 0; определено единственное число a·b (или ab), называемое произведением двух действительных чисел, так что выполняются условия:
определено единственное число a·b (или ab), называемое произведением двух действительных чисел, так что выполняются условия: такое, что a· 1= a для
такое, что a· 1= a для 
 единственное обратное число
единственное обратное число  такое, что
такое, что  ;
; (или a: b) называется частным от деления числа a на число b.
(или a: b) называется частным от деления числа a на число b. .
. ;
; .
.
 такое, что a < c < b v
такое, что a < c < b v
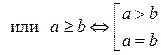
 :
: и
и  , у которых для
, у которых для  и
и  выполняется неравенство
выполняется неравенство 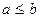 , существует такое число
, существует такое число  , что выполняется соотношение
, что выполняется соотношение  при
при 

 ставится во взаимно однозначное соответствие точка с координатой x на числовой прямой.
ставится во взаимно однозначное соответствие точка с координатой x на числовой прямой.


