Промежутки расширенной числовой прямойПусть
Точки a и b называют концами промежутка; точки x такие, что a < x < b называют внутренними точками промежутка. Если a и b — это числа, т.е. принадлежат Свойство промежутков Промежутки всех типов расширенной числовой прямой обладают следующим свойством: если точки
Окрестности точек числовой прямой Окрестностью конечной точки обозначение окрестности точки В частности, симметричный относительно точки e -окрестность точки х 0 можно описать как множество следующим образом:
Определения e-окрестностей бесконечно удаленных точек:
Пример (e -окрестности точек Запишем e -окрестности некоторых точек, положив e = 1 и e = 0,1:
|
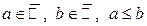. Промежутками расширенной числовой прямой называются следующие множества:
— отрезок числовой прямой;
— интервал числовой прямой;
— полуинтервалы (полуотрезки) числовой прямой.
, и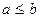 
, то промежуток с концами a и b называют конечным промежутком и число 
называют длиной конечного промежутка (или его мерой).
, принадлежат некоторому промежутку с концами 
, то весь отрезок 
принадлежит этому промежутку. Например, как это показано на рис. 17.
числовой прямой называется любой интервал, содержащий точку 
.
называется e-окрестностью конечной точки 
;
)
, 
, 
, 
;
, 
, 
, 
.
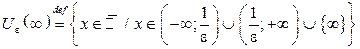
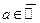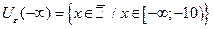