Примеры выполнения операций над множествами
Пример 1 (выполнение операций над конечными множествами) Даны два конечных числовых множества А и В. Изобразить эти множества диаграммой Эйлера-Венна. Записать элементы множеств а)
Решение
Записываем результаты выполнения операций над множествами A и B:
Пример 2 (выполнение операций над бесконечными множествами) Даны два бесконечных числовых множества Записать промежутками множества A, B, Множества
Решение Находим множества А и В и изображаем их элементы на координатной оси:
Для выполнения операций объединения, пересечения и разности множеств удобно множества А и В изобразить на одной координатной прямой (можно и кругами Эйлера):
Теперь выполняем операции над множествами, пользуясь определениями этих операций:
Пример 3 (определение элементов множества) Записать элементы следующих множеств Решение
Ответ:
Пример 4 (множества точек на координатной плоскости) Построить элементы множества Решение
пересечением множеств A 1 и A 2 определяем искомое множество A.
Пример 5 (разбиение множества на подмножества) Дано множество А натуральных чисел от 10 до 25 включительно. Разбить множество А на подмножества по принципу деления его элементов на числа 3 и 2. Решение Записываем множество А списком его элементов:
По признаку деления чисел а на числа 3 и 2 определяются следующие четыре непересекающиеся подмножества:
Очевидно, что множества
Теперь распределяем числа а по множествам
|

 ,
, 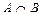 ,
, 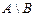 ,
,  ,
,  ,
, 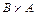 .
. ,
,  ; б)
; б) 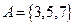 ,
,  .
. Рис. 10
Рис. 10
 ;
;  ;
; ;
;  ;
;

 Рис. 11
Рис. 11
 ;
;  ;
; 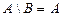 ;
;  ;
;
 ;
;  .
.
 и
и  .
.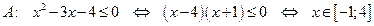

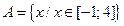 .
.


 .
.



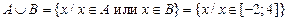 ;
;

 ;
;

 ;
;

 .
.



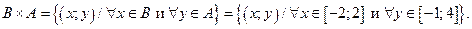
 ,
,  .
.
 .
.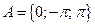 ,
,  .
. на коорд. плоскости XOY.
на коорд. плоскости XOY.




 — это множество точек в полосе между прямыми x = –1 и x = 1, включающее в себя и точки на самих прямых;
— это множество точек в полосе между прямыми x = –1 и x = 1, включающее в себя и точки на самих прямых;
 — это множество точек, расположенных выше прямой y = x; оно включает в себя и точки на самой прямой;
— это множество точек, расположенных выше прямой y = x; оно включает в себя и точки на самой прямой; .
. — множество чисел а, которые делятся на число 3, но не делятся на число 2;
— множество чисел а, которые делятся на число 3, но не делятся на число 2; — множество чисел а, которые делятся на число 2, но не делятся на число 3;
— множество чисел а, которые делятся на число 2, но не делятся на число 3;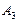 — множество чисел а, которые делятся и на число 3, и на число 2, т.е делятся на число 6;
— множество чисел а, которые делятся и на число 3, и на число 2, т.е делятся на число 6; — множество чисел а, которые не делятся ни на число 3, ни на число 2.
— множество чисел а, которые не делятся ни на число 3, ни на число 2.

 ,
,
 ,
,
 ,
,
 .
.



