Основные обозначения
________________________________________________________ (наименование стройки (ремонтируемого объекта)) Составлена в ценах по состоянию на _________________ 20___г.
Руководитель проектной организации________________________ [подпись (инициалы, фамилия)]
Главный инженер проекта__________________________________ [подпись (инициалы, фамилия)]
Начальник_______________отдела__________________________ (наименование) [подпись (инициалы, фамилия)]
Заказчик_________________________________________________ [должность, подпись (инициалы, фамилия)] Введение
Тема I. Элементы теории множеств § 1. Множества: определения, способы задания, основные операции Содержание 1.1. Основные обозначения. 4 1.2. Способы задания множеств. 5 1.3. Подмножества. 6 1.4. Основные операции над множествами.. 7 1.5. Примеры выполнения операций над множествами.. 10 1.6. Упражнения для самостоятельной работы.. 14 Вопросы для самопроверки.. 16 Глоссарий 17
Основные обозначения Далее будут использоваться следующие обозначения: A, B, C, X, Y, … — множества;
¥ — множество натуральных чисел; ¢ — множество целых чисел;
a, b, c, x, y, … — элементы множеств;
def — «по определению»; / или: — «таких, что»; È — знак объединения множеств; Ç — знак пересечения множеств; \ — знак разности множеств; Ì, É — знаки включения множеств; A ´ B —декартово произведение множества A на множество B; B ' A — дополнение к множеству B в множестве A; { — логическое «и»; [ — логическое «или»; w — начало доказательства; v — конец доказательства.
|

 — множество действительных чисел;
— множество действительных чисел; — множество рациональных чисел;
— множество рациональных чисел; — элемент a принадлежит множеству A;
— элемент a принадлежит множеству A; — элемент a не принадлежит множеству A;
— элемент a не принадлежит множеству A; — пустое множество, т.е. множество, которое не содержит ни одного
— пустое множество, т.е. множество, которое не содержит ни одного  — знак всеобщности («для всех», «для любых», «для каждого»);
— знак всеобщности («для всех», «для любых», «для каждого»); — знак существования («существует»);
— знак существования («существует»);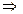 — знак следствия («отсюда следует»);
— знак следствия («отсюда следует»); — знак следствия в обе стороны, знак взаимно однозначного
— знак следствия в обе стороны, знак взаимно однозначного


