Упражнения для самостоятельной работы. 1. Взяв e = 0,5 и e = 0,05, запишите e-окрестности и проколотые e-окрестности следующих точек расширенной числовой прямой:
1. Взяв e = 0,5 и e = 0,05, запишите e-окрестности и проколотые e-окрестности следующих точек расширенной числовой прямой: 2. Постройте на координатной плоскости XOY следующие множества: 3. Запишите элементы следующих множеств: Ответы к упражнениям для самостоятельной работы
3.
Вопросы для самопроверки Что называется расширенным множеством действительных чисел или расширенной числовой прямой? Что называется бесконечно удаленными точками расширенной числовой прямой? Что называется конечными точками числовой прямой? Что называется промежутками расширенной числовой прямой? Что такое отрезок числовой прямой? Что такое интервал числовой прямой? Что такое полуинтервалы (полуотрезки) числовой прямой? Что называется концами промежутка? Что называется внутренними точками промежутка? Что называется окрестностью конечной точки? Что называется e-окрестностью конечной точки? Что такое определения e-окрестностей бесконечно удаленных точек? Что такое свойства окрестностей? Что называется проколотой окрестностью точки? Что называется системой вложенных отрезков? Сформулируйте теорему о пересечении системы вложенных отрезков. Глоссарий e-окрестностью конечной точки называется…(стр. 31) бесконечно удаленными точками расширенной числовой прямой называется…(стр. 30) внутренними точками промежутка называется…(стр. 30) интервал числовой прямой это…(стр. 30) конечными точками числовой прямой называется…(стр. 30) концами промежутка называется…(стр. 30) окрестностью конечной точки называется…(стр. 31) определения e-окрестностей бесконечно удаленных точек называется…(стр. 31) отрезок числовой прямой это…(стр. 30) полуинтервалы (полуотрезки) числовой прямой это…(стр. 30) проколотой окрестностью точки называется…(стр. 33) промежутками расширенной числовой прямой называется…(стр. 30) расширенным множеством действительных чисел или расширенной числовой прямой называется…(стр. 29) свойства окрестностей это…(стр. 32) системой вложенных отрезков называется…(стр. 34)
|
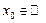, x 0 = 0, +¥, –¥, ¥. 
, 
, 
, 
, 
, 
.
, 
, 
.
,
,
,
,
,
,
,
,
;
,
,
;
;
.
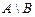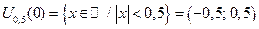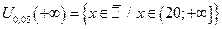
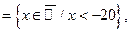
