Дано множество точек на координатной прямой. Требуется охарактеризовать его ограниченность, указать точные грани и экстремумы множества.
а)  ; б)
; б)  .
.
Решение
а) Записываем элементы множества 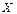 и изображаем их точками на координатной оси:
и изображаем их точками на координатной оси:
Описываем ограниченность множества 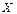 , пользуясь определениями данного параграфа:
, пользуясь определениями данного параграфа:
– ограничено сверху, т.к. существуют числа  такие, что для
такие, что для  выполняется неравенство
выполняется неравенство  ;
;
– не ограничено снизу, т.к. для  найдется
найдется  такой, что
такой, что  ;
;
– неограниченное множество, т.к. не ограничено снизу;
– точная верхняя грань  , т.к. число 3 является наименьшим из всех чисел
, т.к. число 3 является наименьшим из всех чисел  , ограничивающих множество
, ограничивающих множество 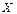 сверху;
сверху;
– точная нижняя грань  – не существует, или
– не существует, или  , т.к. множество
, т.к. множество 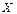 не ограничено снизу;
не ограничено снизу;
– максимум множества  , т.к. 3 – это точная верхняя грань множества
, т.к. 3 – это точная верхняя грань множества 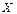 и она принадлежит
и она принадлежит 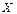 ;
;
– минимум множества  – не существует, т.к. нет точной нижней грани, следовательно, она не может принадлежать
– не существует, т.к. нет точной нижней грани, следовательно, она не может принадлежать 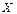 .
.
б) Решаем неравенство, определяющее множество  , и изображаем множество
, и изображаем множество  точками на координатной оси:
точками на координатной оси:







 ;
;
знаки дроби  определяем методом интервалов:
определяем методом интервалов:
Теперь описываем ограниченность множества  :
:
– ограниченное сверху, т.к. существуют числа  такие, что
такие, что  для
для  ;
;
– ограниченное снизу, т.к. существуют числа  такие, что
такие, что  для
для  ;
;
– ограниченное, т.к. ограничено сверху и ограничено снизу;
–  , т.к. число 0 является наименьшим из всех чисел
, т.к. число 0 является наименьшим из всех чисел  , ограничивающих множество
, ограничивающих множество  сверху;
сверху;
–  , т.к. число –2 является наибольшим из всех чисел
, т.к. число –2 является наибольшим из всех чисел  , ограничивающих множество
, ограничивающих множество  снизу;
снизу;
–  не существует, т.к. число
не существует, т.к. число  не принадлежит
не принадлежит  ;
;
–  , т.к. число
, т.к. число  принадлежит
принадлежит  .
.

 ; б)
; б)  .
.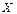 и изображаем их точками на координатной оси:
и изображаем их точками на координатной оси:

 такие, что для
такие, что для  выполняется неравенство
выполняется неравенство  ;
; найдется
найдется  такой, что
такой, что  ;
; , т.к. число 3 является наименьшим из всех чисел
, т.к. число 3 является наименьшим из всех чисел  – не существует, или
– не существует, или  , т.к. множество
, т.к. множество  , т.к. 3 – это точная верхняя грань множества
, т.к. 3 – это точная верхняя грань множества  – не существует, т.к. нет точной нижней грани, следовательно, она не может принадлежать
– не существует, т.к. нет точной нижней грани, следовательно, она не может принадлежать  , и изображаем множество
, и изображаем множество 





 ;
; определяем методом интервалов:
определяем методом интервалов:
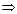

 такие, что
такие, что  для
для  ;
; такие, что
такие, что  для
для  , т.к. число 0 является наименьшим из всех чисел
, т.к. число 0 является наименьшим из всех чисел  , т.к. число –2 является наибольшим из всех чисел
, т.к. число –2 является наибольшим из всех чисел  не существует, т.к. число
не существует, т.к. число  не принадлежит
не принадлежит  , т.к. число
, т.к. число  принадлежит
принадлежит 


