Пусть задана функция  и задано множество
и задано множество 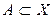 .
.
Образом множества А при отображении f называется множество всех 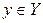 , являющихся значениями функции f в точках
, являющихся значениями функции f в точках 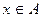 .
.
Обозначение: 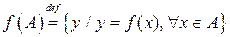 .
.
В частности, 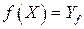 , то есть образом множества задания функции является множество ее значений.
, то есть образом множества задания функции является множество ее значений.
Если множество 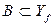 , то множество A всех значений аргумента х, для которых
, то множество A всех значений аргумента х, для которых 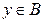 , называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:
, называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:

 .
.
Пример 4 (образы и прообразы множеств при различных отображениях)
1) Множество 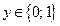 является образом множества
является образом множества 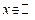 при отображении функцией
при отображении функцией
Дирихле; множество 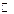 является прообразом множества
является прообразом множества 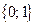 при отображении той же функцией;
при отображении той же функцией;
2) 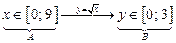
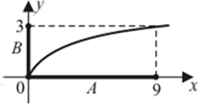
| 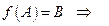 В — это образ множества А при отображении функцией В — это образ множества А при отображении функцией 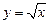 ,
A — это прообраз множества B при этом отображении функцией ,
A — это прообраз множества B при этом отображении функцией 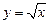 ; ;
|
3) найдем образ множества 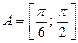 при отображении функцией
при отображении функцией 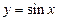 :
:
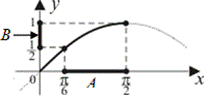
|  ,
то есть ,
то есть 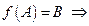 В — это образ мно- жества А при отображении функцией В — это образ мно- жества А при отображении функцией 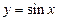 ; ;
|
4) найдем образ множества 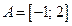 при отображении функцией при отображении функцией 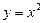 . .
|
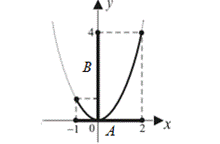
| 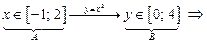
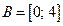 или или 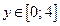 — это образ множества А при отображении функцией — это образ множества А при отображении функцией 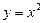 ; ;
|
5) найдем прообраз множества  при отображении функцией
при отображении функцией 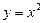 :
:
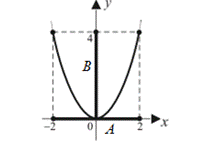
| 
 — это прообраз множества В при отображении функцией — это прообраз множества В при отображении функцией 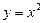 . .
|
Понятие многозначного отображения
Отображение  называется многозначным отображением, если существуют
называется многозначным отображением, если существуют  такие, что им соответствуют более одного элемента
такие, что им соответствуют более одного элемента 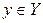 ,(рис. 32).
,(рис. 32).
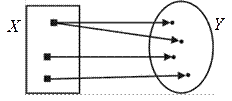
Рис. 32
Многозначные функции рассматривать будем пока только в исключительных случаях, поэтому по умолчанию любая функция 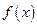 считается задающей однозначное отображение.
считается задающей однозначное отображение.

 и задано множество
и задано множество 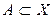 .
.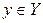 , являющихся значениями функции f в точках
, являющихся значениями функции f в точках 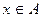 .
.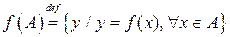 .
.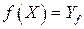 , то есть образом множества задания функции является множество ее значений.
, то есть образом множества задания функции является множество ее значений.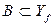 , то множество A всех значений аргумента х, для которых
, то множество A всех значений аргумента х, для которых 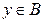 , называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:
, называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:
 .
.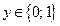 является образом множества
является образом множества 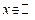 при отображении функцией
при отображении функцией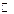 является прообразом множества
является прообразом множества 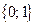 при отображении той же функцией;
при отображении той же функцией;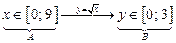

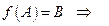 В — это образ множества А при отображении функцией
В — это образ множества А при отображении функцией 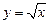 ,
A — это прообраз множества B при этом отображении функцией
,
A — это прообраз множества B при этом отображении функцией 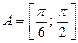 при отображении функцией
при отображении функцией 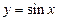 :
:
 ,
то есть
,
то есть 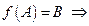 В — это образ мно- жества А при отображении функцией
В — это образ мно- жества А при отображении функцией 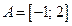 при отображении функцией
при отображении функцией 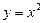 .
.

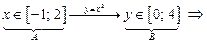
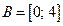 или
или 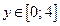 — это образ множества А при отображении функцией
— это образ множества А при отображении функцией  при отображении функцией
при отображении функцией 
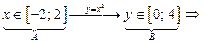
 — это прообраз множества В при отображении функцией
— это прообраз множества В при отображении функцией  называется многозначным отображением, если существуют
называется многозначным отображением, если существуют  такие, что им соответствуют более одного элемента
такие, что им соответствуют более одного элемента 
 считается задающей однозначное отображение.
считается задающей однозначное отображение.


