Пусть имеем отображение общего вида  , причем
, причем 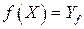 , где
, где  , (рис. 33).
, (рис. 33).
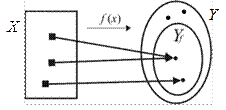
Рис. 33
Если рассмотреть отображение 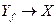 , то оно называется обратным отображением по отношению к отображению
, то оно называется обратным отображением по отношению к отображению 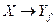 . Понятно, что обратное отображение является, вообще говоря, многозначным.
. Понятно, что обратное отображение является, вообще говоря, многозначным.
Если отображение  является взаимно однозначным (биективным), то обратное ему отображение
является взаимно однозначным (биективным), то обратное ему отображение  является также взаимно однозначным отображением множества
является также взаимно однозначным отображением множества  на множество X, (рис. 34); в этом случае обратное отображение определяет функцию
на множество X, (рис. 34); в этом случае обратное отображение определяет функцию  , которая называется обратной функцией по отношению к функции
, которая называется обратной функцией по отношению к функции  .
.
 Рис. 34
Рис. 34
| если  — биекция, то — биекция, то  — тоже биекция. — тоже биекция.
|
Очевидно, что функция 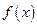 является обратной по отношению к функции
является обратной по отношению к функции  , а обе эти функции f и
, а обе эти функции f и 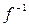 называются взаимно обратными функциями.
называются взаимно обратными функциями.
Пример 5 (взаимно обратные функции)
Подробнее о взаимно обратных функциях изложено в §8 данного конспекта.
Суперпозиция отображений (сложная функция)
Если заданы два отображения  и
и  , то отображение
, то отображение  , ставящее в соответствие любому элементу
, ставящее в соответствие любому элементу 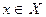 единственный элемент
единственный элемент 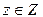 , называется суперпозицией отображений f и g(другие названия: композиция отображений, сложное отображение).
, называется суперпозицией отображений f и g(другие названия: композиция отображений, сложное отображение).
Иллюстрация к сложному отображению приведена на рис. 35.
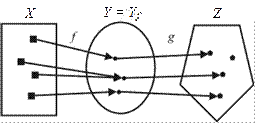
Рис. 35
Обозначение суперпозиции отображений:  или
или 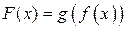 .
.
Пример 6 (сложные отображения)
| 1)
| 
|
| 
|
 ;
;
2) 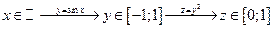
Запись сложных отображений как сложных функций:
 .
.
Сложное отображение (сложная функция) может получаться суперпозицией любого количества отображений.
Пример 7 (составление сложных функций)
1)  — сложная функция
— сложная функция
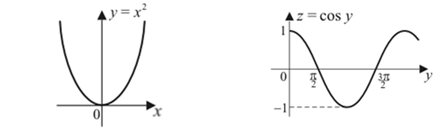
 ;
;
2) 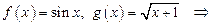

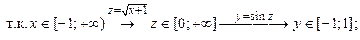
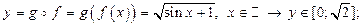
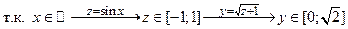
3) 




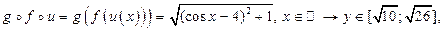


 ,
,
 .
.

 , причем
, причем 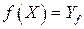 , где
, где  , (рис. 33).
, (рис. 33).
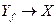 , то оно называется обратным отображением по отношению к отображению
, то оно называется обратным отображением по отношению к отображению 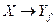 . Понятно, что обратное отображение является, вообще говоря, многозначным.
. Понятно, что обратное отображение является, вообще говоря, многозначным. является взаимно однозначным (биективным), то обратное ему отображение
является взаимно однозначным (биективным), то обратное ему отображение  является также взаимно однозначным отображением множества
является также взаимно однозначным отображением множества  на множество X, (рис. 34); в этом случае обратное отображение определяет функцию
на множество X, (рис. 34); в этом случае обратное отображение определяет функцию  , которая называется обратной функцией по отношению к функции
, которая называется обратной функцией по отношению к функции  Рис. 34
Рис. 34
 — биекция, то
— биекция, то  — тоже биекция.
— тоже биекция.
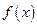 является обратной по отношению к функции
является обратной по отношению к функции  , а обе эти функции f и
, а обе эти функции f и 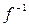 называются взаимно обратными функциями.
называются взаимно обратными функциями.
 и
и  ;
;

 и
и 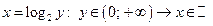 .
.
 и
и  , то отображение
, то отображение  , ставящее в соответствие любому элементу
, ставящее в соответствие любому элементу 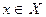 единственный элемент
единственный элемент 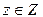 , называется суперпозицией отображений f и g(другие названия: композиция отображений, сложное отображение).
, называется суперпозицией отображений f и g(другие названия: композиция отображений, сложное отображение).
 или
или 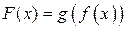 .
.

 ;
;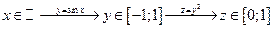
 .
. — сложная функция
— сложная функция
 ;
;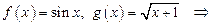

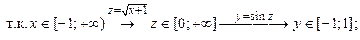
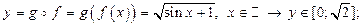
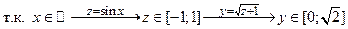




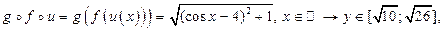

 ,
, .
.


