Основные свойства счетных множеств
Нетрудно доказать или интуитивно пояснить несколько основных свойств счетных множеств. 1. Множество останется счетным, если в него добавить один элемент или удалить из него один элемент. Множество останется счетным, если его объединить с любым конечным множеством или вычесть из него конечное множество. 2. Объединением конечного числа счетных множеств получается счетное множество. 3. Объединение счетного количества счетных множеств является счетным множеством. 4. Из любого бесконечного множества всегда можно выделить счетное подмножество, при этом мощность бесконечного множества не изменится. 5. Счетные множества имеют наименьшую мощность среди всех бесконечных множеств.
w 1. Добавление или удаление одного элемента (или любого конечного числа элементов) приводит просто к перенумерации элементов счетного множества. Например, рассмотрим
2. Рассмотрим объединение двух счетных множеств:
т.е. объединение двух cчетных множеств есть счетное множество. На любое конечное число счетных множеств утверждение распространяется по свойству ассоциативности операции объединения:
3. Иллюстрацией к свойству объединения счетного числа счетных множеств может быть процедура нумерации «по квадратам» элементов множества положительных рациональных чисел на рис. 38: в каждой строке первоначальной таблицы этих чисел было счетное количество элементов и количество строк также было счетным; следовательно вся таблица представляла собой объединение счетного количества счетных множеств, и было доказано, что это объединение является счетным.
4. Чтобы выделить из бесконечного множества
5. Утверждение о том, что счетные множества имеют наименьшую мощность среди всех бесконечных множеств, следует из следующих двух фактов: 1) любая бесконечная часть множества натуральных чисел является счетной, поэтому не может существовать бесконечное множество, мощность которого была бы меньше мощности счетного множества; 2) в каждом бесконечном множестве есть счетное подмножество, поэтому мощность счетного множества не больше мощности любого бесконечного множества, то есть эта мощность — самая маленькая из мощностей бесконечных множеств. v
|

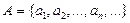 – счетное множество,
– счетное множество, – конечное множество,
– конечное множество,  ; тогда
; тогда  , где
, где 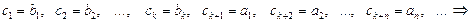
 – счетное множество.
– счетное множество. ,
, 
 – счетное множество, если
– счетное множество, если  – счетные.
– счетные. счетное подмножество
счетное подмножество 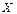 , нужно поступить так: выберем из множества
, нужно поступить так: выберем из множества 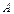 один элемент
один элемент  - это можно сделать, так как множество
- это можно сделать, так как множество 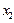 и т.д. В результате мы извлечем из бесконечного множества
и т.д. В результате мы извлечем из бесконечного множества 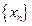 . Далее можно показать, что в множестве
. Далее можно показать, что в множестве  будет совпадать с мощностью множества
будет совпадать с мощностью множества 


