Тема II. Числовые функции
§ 7. Числовая функция: определение, способы задания, график Содержание 7.1. Определение числовой функции.. 74 7.2. Сужение функции.. 76 7.3. Способы задания функции.. 76 7.4. Явно или неявно заданные функции.. 77 7.5. Параметрически заданные функции.. 79 7.6. График функции.. 81 7.7. Примеры построения графиков функций.. 82 7.8. Упражнения для самостоятельной работы.. 85 Вопросы для самопроверки.. 87 Глоссарий ……………………………………………………………………………87
Определение числовой функции
Обозначения: Здесь x — это независимая переменная, или аргумент; переменные x и y связаны функциональной зависимостью f.
Если обозначить через X – множество значений, которые может принимать переменная x, Y – множество значений, которые принимает переменная y при то функциональная зависимость между переменными x и y адает отображение числового множества X на числовое множество Y, при котором каждому элементу
Рис. 40 В отличие от более общего определения функции как отображения множеств, состоящих из элементов любой природы, числовая функция задает отображение множества X, элементами которого являются числа, на множество Y, элементами которого тоже являются числа. Кроме того, далее будем считать, что множество Y — это есть множество значений функции, так что отображение Множество X задания функции и множество Y значений функции для числовых функций традиционно называют областью определения функции (ООФ)и областью значений функции (ОЗФ). Значение функции в точке Если задано отображение множеств функцией Если x 0 — это фиксированное значение аргумента x, то значение функции в точке x 0 обозначается следующими символами:
Например,
|

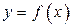 или
или 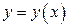 или
или  или
или  или
или 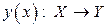 .
.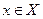 ,
,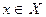 ставится в соответствие единственный элемент множества Y, (рис. 40).
ставится в соответствие единственный элемент множества Y, (рис. 40).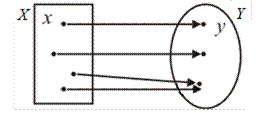
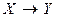 является сюръекцией.
является сюръекцией. , то элементы множеств X и Y называются точками. Символом
, то элементы множеств X и Y называются точками. Символом 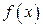 обозначается при этом как сама функция, так и элемент
обозначается при этом как сама функция, так и элемент 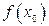 или
или  или
или 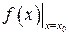 или
или 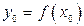 .
.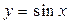
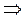
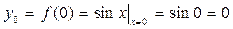 ;
;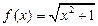
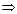
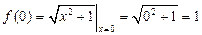 ,
, 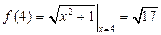 .
.


