Если формула, связывающая аргумент x и функцию y, имеет вид
 ,
,
то переменная y называется явно заданной функцией переменной x.
Например, явно заданными являются функции  ,
,  .
.
Если формула, связывающая аргумент x и функцию у, записана в виде уравнения 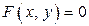 , то определяемая из этого уравнения переменная
, то определяемая из этого уравнения переменная  называется функцией, заданной неявно.
называется функцией, заданной неявно.
Пример (неявно заданные функции)
1) Уравнение  задает неявно функцию
задает неявно функцию  ;
;
2) уравнение  задает неявно функцию
задает неявно функцию  ;
;
3) уравнение  задает неявно две функции
задает неявно две функции  ;
;
4) уравнение  задает неявно бесконечное множество функций
задает неявно бесконечное множество функций 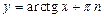 ,
,  .
.
Из примеров видно, что если уравнение 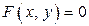 удается решить относительно у, то осуществляется переход от неявно заданной функции к ее явному заданию
удается решить относительно у, то осуществляется переход от неявно заданной функции к ее явному заданию 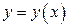 . При этом часто получается многозначная функция, которую всегда можно рассматривать как совокупность однозначных функций (совокупность однозначных ветвей многозначной функции).
. При этом часто получается многозначная функция, которую всегда можно рассматривать как совокупность однозначных функций (совокупность однозначных ветвей многозначной функции).
Например, 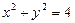
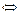

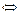
 ;
;

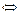
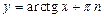 ,
, 
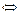

Однако на практике решить уравнение 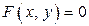 относительно переменной у получается далеко не всегда или это решение получается слишком громоздким. Например, уравнение
относительно переменной у получается далеко не всегда или это решение получается слишком громоздким. Например, уравнение  нельзя решить относительно y. Поэтому в этих случаях приходится работать с функциями, имеющими только неявное задание.
нельзя решить относительно y. Поэтому в этих случаях приходится работать с функциями, имеющими только неявное задание.
Замечание (к неявному заданию функций)
В уравнении  переменные x и y входят равноправно, поэтому можно считать, что это уравнение задает неявно функцию
переменные x и y входят равноправно, поэтому можно считать, что это уравнение задает неявно функцию  или функцию
или функцию 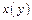 .
.
Например, 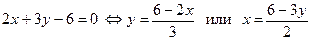 .
.

 ,
, ,
,  .
.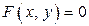 , то определяемая из этого уравнения переменная
, то определяемая из этого уравнения переменная  называется функцией, заданной неявно.
называется функцией, заданной неявно. задает неявно функцию
задает неявно функцию  ;
; задает неявно функцию
задает неявно функцию  ;
; задает неявно две функции
задает неявно две функции  ;
; задает неявно бесконечное множество функций
задает неявно бесконечное множество функций 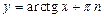 ,
,  .
.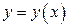 . При этом часто получается многозначная функция, которую всегда можно рассматривать как совокупность однозначных функций (совокупность однозначных ветвей многозначной функции).
. При этом часто получается многозначная функция, которую всегда можно рассматривать как совокупность однозначных функций (совокупность однозначных ветвей многозначной функции).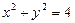
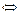
 ;
;

 нельзя решить относительно y. Поэтому в этих случаях приходится работать с функциями, имеющими только неявное задание.
нельзя решить относительно y. Поэтому в этих случаях приходится работать с функциями, имеющими только неявное задание. переменные x и y входят равноправно, поэтому можно считать, что это уравнение задает неявно функцию
переменные x и y входят равноправно, поэтому можно считать, что это уравнение задает неявно функцию  или функцию
или функцию 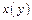 .
.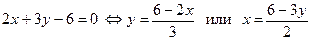 .
.


