Область определения и область значений функции
Областью определения числовой функции (ООФ) ООФ – это основная характеристика любой функции, с учетом которой исследуются все остальные характеристики; ООФ находится чаще всего как подмножество X множества действительных чисел ООФ может находиться по смыслу функции приняты и другие обозначения ООФ, например, D(f) или D(y).
Областью значений числовой функции (ОЗФ) ОЗФ – это вспомогательная характеристика функции, которая вполне определяется после построения графика функции. До того, как график построен, ОЗФ может быть найдена только в отдельных случаях, когда это помогают сделать известные свойства основных элементарных функций, с помощью которых записана исследуемая функция. Для ОЗФ приняты также обозначения E(f) или E(y). Пример (нахождение ООФ и ОЗФ) Найти область определения и область значений в каждой из следующих функций: 1) ОЗФ: 2) ООФ записана из ограничения по делению: на ноль делить нельзя; ОЗФ можно найти только после построения графика функции; 3) ООФ определена операцией извлечения корня квадратного, которая имеет смысл только для неотрицательных чисел; ОЗФ: 4) здесь ООФ учитывает ограничения операции логарифмирования (логарифмы существуют только от положительных чисел) и операции деления (на ноль делить нельзя); ОЗФ определяется после построения графика функции; 5) здесь ООФ записана по смыслу задания функции; ОЗФ: 6) последовательность с общим членом здесь ООФ записана по смыслу задания функции; ОЗФ: 7) Таким образом, в качестве ООФ и ОЗФ
|

 называется множество числовых значений, которые может принимать аргумент x, так чтобы функция имела смысл.
называется множество числовых значений, которые может принимать аргумент x, так чтобы функция имела смысл. , на котором выполнимы все операции, определяющие значение функции y по значению ее аргумента x; в этом случае ООФ называют естественной областью определения функции и она совпадает с областью допустимых значений (ОДЗ) для пенременной
, на котором выполнимы все операции, определяющие значение функции y по значению ее аргумента x; в этом случае ООФ называют естественной областью определения функции и она совпадает с областью допустимых значений (ОДЗ) для пенременной  в выражении f (x);
в выражении f (x); называется множество числовых значений, которые принимает функция y, если ее аргумент
называется множество числовых значений, которые принимает функция y, если ее аргумент  .
.
 ООФ:
ООФ:  или
или  ;
; , так как это сложная функция, полученная суперпозицией двух функций
, так как это сложная функция, полученная суперпозицией двух функций  :
:  и
и  ;
;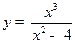
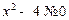
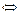

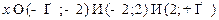 ;
;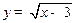


 ;
; , так как корень квадратный
, так как корень квадратный  принимает все неотрицательные значения, если
принимает все неотрицательные значения, если 

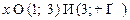 ;
; ,
, 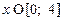
 – определена по графику функции
– определена по графику функции 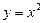 ;
; может рассматриваться как функция натурального аргумента n, то есть
может рассматриваться как функция натурального аргумента n, то есть 
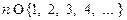 ;
; ;
; ООФ:
ООФ: 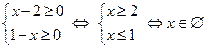 ; ОЗФ:
; ОЗФ:  .
. могут получиться любые множества: непрерывные или дискретные, бесконечные или конечные, в том числе может получиться пустое множество.
могут получиться любые множества: непрерывные или дискретные, бесконечные или конечные, в том числе может получиться пустое множество.


