Параметрически заданные функцииСвязь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
В этом случае функция
Например, в механике при описании движения точки по некоторой траектории От параметрически заданной функции можно перейти к явной или неявной форме её задания, если удаётся исключить параметр t. Пример (параметрически заданные функции) 1. Таким образом, система
2. Таким образом, система
3.
Из последнего примера хорошо видно, что для одной и той же функции можно записать несколько вариантов параметрических уравнений, вводя по-разному параметр.
Выполнить исключение параметра из системы параметрических уравнений не всегда возможно, поэтому нужно уметь работать и с функциями, имеющими только параметрические задания.
|
, где 
– это параметр, 
.
называется функцией, заданной параметрически.
Рис. 41
, т. е. задавать функцию 
или 
.
задаются абсцисса и ордината движущейся точки как функции времени t, (рис. 41).
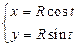— это есть параметрические уравнения окружности радиуса R с центром в начале координат и, следовательно, задают две функции 
, 
:
на нижней полуокружности
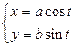— это есть параметрические уравнения эллипса с полуосями a и b и с центром в начале координат, они задают две функции:
;
на нижней половине эллипса
.
— уравнение параболы;
—
