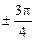Примеры построения графиков функций
1. Построить график функции Такая функция, задаваемая явно, но несколькими формулами, называется кусочно заданной функцией. Решение Чтобы построить график этой кусочно заданной функции, нужно построить графики известных функций выделить сужение каждой из этих функций на указанное множество значений x;
объединить сужения в общий график.
Таким образом, график кусочно заданной функции получается компиляцией (объединением, склеиванием) «кусков» графиков известных функций.
2. Перейти от неявно заданной функции y(x) уравнением Решение Решаем данное уравнение относительно y:
Получили равенство, которое каждому значению
3. Построить график функции Решение По определению модулей имеем, что
Преобразуем данную функцию, раскрыв оба модуля на каждом из промежутков знакопостоянства подмодульных выражений:
Строим график получившейся кусочно-заданной функции:
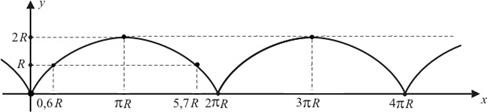
4. Построить график функции, заданной параметрически Линия, описываемая этими уравнениями, называется циклоидой. Решение Построение графика любой функции, заданной параметрически, проводится поточечно с помощью таблицы соответствующих значений параметра, аргумента и функции.
Эта функция является периодической с наименьшим периодом Известно геометрическое определение циклоиды как линии, которую описывает фиксированная точка окружности радиуса R, если окружность катится без скольжения по прямой:
фиксированная точка окружности в начальный момент времени.
5. Построить график функции Решение Построение линии в полярной системе координат выполняется по точкам с помощью таблицы соответствующих друг другу значений аргумента и функции. При построении таблицы учтем, что функция
Линия, описываемая уравнением
|


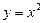 ,
,  ,
, 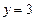 ;
;





 :
:

 .
.
 к явному заданию и построить график.
к явному заданию и построить график. , где
, где  .
.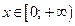 ставит в соответствие два значения y. Можно было бы его истолковать как двузначную функцию. Но функциональная зависимость по определению однозначная, т. к. этим определением каждому значению x ставится в соответствие единственное значение y. Поэтому нужно перейти от якобы двузначной функции к совокупности двух однозначных функций:
ставит в соответствие два значения y. Можно было бы его истолковать как двузначную функцию. Но функциональная зависимость по определению однозначная, т. к. этим определением каждому значению x ставится в соответствие единственное значение y. Поэтому нужно перейти от якобы двузначной функции к совокупности двух однозначных функций:
 – графиком является верхняя ветвь параболы
– графиком является верхняя ветвь параболы 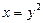 ,
,
 – графиком является нижняя ветвь параболы
– графиком является нижняя ветвь параболы  .
.


 :
:

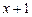
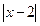 :
:



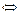
 .
.







 ,
, 




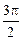
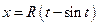








 .
.


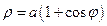 в полярной системе координат.
в полярной системе координат. является четной, поэтому
является четной, поэтому  .
.