Четность, нечетность функций
Функция
График четной функции всегда имеет осевую симметрию относительно оси функции, (рис.45). Функция
График нечетной функции всегда имеет центральную симметрию относительно начала координат, (рис.46).
Рис.45 Рис.46 Пример (исследование функций на четность) Исследовать следующие функции на четность: 1) Решение 1) вычисляем равенство 2) ООФ является симметричной относительно точки x = 0; вычисляем равенство 3) вычисляем здесь не выполняется ни одно из равенств 4) ООФ не является симметричной относительно точки x = 0, поэтому свойством четности или нечетности эта функция обладать не может. Следовательно, она относится к функциям общего вида, которые не являются ни четными, ни нечетными. Ответ: 1) функция 2) функция 3) функция 4) функция
|

 называется четной функцией, если выполняются следующие два условия:
называется четной функцией, если выполняются следующие два условия:



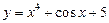 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
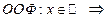 ООФ симметрична относительно точки x = 0;
ООФ симметрична относительно точки x = 0;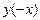 , используя четность основных элементарных функций
, используя четность основных элементарных функций 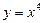 и
и  :
:  ;
; выполняется для
выполняется для 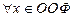 , поэтому данная функция является четной, ее график будет симметричным относительно оси OY;
, поэтому данная функция является четной, ее график будет симметричным относительно оси OY;
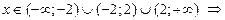
 ,
,  :
:
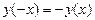 выполняется при
выполняется при  – есть симметрия ООФ относительно точки x = 0;
– есть симметрия ООФ относительно точки x = 0;

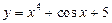 является четной;
является четной; не является ни четной, ни нечетной;
не является ни четной, ни нечетной;


