Решение задачи о нахождении обратной функции
Постановка задачи Для каждой из следующих функций 1. Решение Строим график функции
Для нахождения обратной функции сначала разрешаем уравнение
получилась обратная функция в виде
Теперь в обратной функции переобозначаем аргумент на x, а функцию на y:
в результате получилась обратная функция в искомом виде:
Строим графики обеих взаимно обратных функций Ответ: если то
2.
Выражаем x через y из равенства, задающего данную функцию:
переобозначим y на x, а x на y: это и есть искомая обратная функция.
Строим графики обеих взаимно обратных функций в одной системе координат, подтверждаем их симметричность относительно прямой
Ответ: если то
|
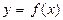найти обратную функцию 
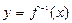. Построить графики обеих функций в одной системе координат, записать для каждой функции область определения и область значений:
; 2. 
.
и проверяем биективность отображения множеств, описываемого этой функцией:
, имеющей вершину в точке (-1;2); по графику определяем, что имеем биективное отображение
, следовательно обратная функция существует.
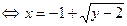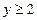, где 
;
.
, где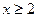 
;
.
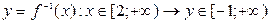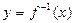в одной системе координат и подтверждаем их симметричность относительно прямой y = x.
,
;
, 
; 
, 
.
;
;
;
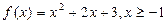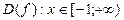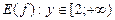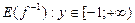и записываем ответ.
,
;
, 
;
.
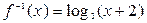