Алгебраические и трансцендентные функции
В множестве элементарных функций выделяют алгебраические и трансцендентные функции. Алгебраическими функциями называют целые многочлены, рациональные дроби и иррациональные функции. Например, Трансцендентными функциями называют элементарные функции, не являющиеся алгебраическими. Например, Среди алгебраических функций выделяются целые многочлены и рациональные дроби. Целым многочленом (полиномом) степени n относительно переменной x называется функция следующего вида: здесь
Примеры (целые многочлены) 1) 2) 3) 4) График квадратичной функции Функция Число Графиком квадратичной функции является парабола, ее положение относительно координатных осей определяется знаком старшего коэффициента a и значением дискриминанта D (см. таблицу на рис. 59).
Рис.59 Здесь x 1, x 2 — это нули квадратичной функции, Иррациональные функции — это такие алгебраические функции Например, 1)
|
; 
; 
.
; 
; 
.
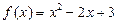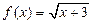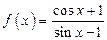(1)
— степень многочлена;
– коэффициенты многочлена (числа или параметры);
– старший коэффициент.
– многочлен первой степени;
— квадратный трехчлен, или квадратичная функция;
— многочлен нулевой степени;
- многочлен 10-й степени.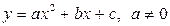
называется квадратичной функцией.
называется дискриминантом квадратного трехчлена.
Þ 
, если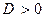 
;
— абсцисса вершины параболы (точка экстремума);
— ордината вершины (экстремум квадратичной функции).
, у которых выражение 
содержит корни различных степеней.
; 2) 
; 3) 
.
