Рациональные дроби
Рациональной дробью (рациональной функцией)называется функция, записанная как отношение двух целых многочленов: где
Например, Рациональная функция (2) называется правильной рациональной дробью, если степень многочлена в числителе меньше степени многочлена в знаменателе, то есть если Например, в предыдущем примере:
Делением многочлена на многочлен «в столбик» любую неправильную рациональную дробь можно представить в виде суммы целого многочлена и правильной рациональной дроби. Эта процедура называется выделением целой части в неправильной рациональной дроби. Примеры (выделение целой части в неправильной рациональной дроби)
Простейшими (элементарными) рациональными дробями называются следующие правильные дроби вида I-IV:
Справедливо следующее важное свойство правильных рациональных дробей.
Примеры (разложение правильных рациональных дробей на сумму 1) 2) 3) 4) Вычислим неопределенные коэффициенты в разложениях 1) и 3): 1) так как тождественно равны две дроби с одинаковыми знаменателями, то тождественно равны их числители: 1 º A(x + 3 ) + B(x – 2 ); (*) вычисляем числа А и В, используя метод частных значений x, суть которого состоит в следующем: тождественное равенство двух многочленов относительно x означает, что равны значения этих многочленов при любых частных значениях x; при x = 2 получим при x = – 3 получим вычислив неопределенные коэффициенты, обязательно нужно делать проверку получившемуся разложению:
таким образом, неопределенные коэффициенты вычислены верно, и разложение правильной рациональной дроби на простейшие дроби имеет вид:
3)
для нахождения чисел А, В, С можно также использовать способ приравнивания коэффициентов при одинаковых степенях x, который основан на следующем свойстве целых многочленов: тождественное равенство двух многочленов означает совпадение их коэффициентов при одинаковых степенях x; в рассматриваемом примере в последнем равенстве справа раскроем скобки и приведем подобные по x:
в результате получилась система трёх линейных уравнений относительно трёх неизвестных А, В, С. Решаем эту систему:
таким образом, неопределенные коэффициенты вычислены. Подставляем их в искомое разложение и обязательно делаем проверку:
Ответ:
|

 , (2)
, (2) ,
,  .
.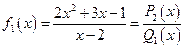 ;
;  ;
;  .
. , и называется неправильной рациональной дробью, если степень многочлена в числителе больше или равна степени многочлена в знаменателе, то есть если
, и называется неправильной рациональной дробью, если степень многочлена в числителе больше или равна степени многочлена в знаменателе, то есть если  .
. — правильная рациональная дробь,
— правильная рациональная дробь, и
и  — это неправильные рациональные дроби.
— это неправильные рациональные дроби. ,
,

 ,
,

 II.
II. 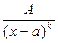 , k = 2, 3…
, k = 2, 3…
 ,
IV.
,
IV.  , k = 2, 3,…
, k = 2, 3,…
 .
.
 записать дробь вида I:
записать дробь вида I:  для кратного линейного множителя
для кратного линейного множителя  записать сумму
записать сумму  дробей вида I и
дробей вида I и
 II:
для квадратичного множителя
II:
для квадратичного множителя  записать дробь вида III:
записать дробь вида III:
 ;
для кратного квадратичного множителя
;
для кратного квадратичного множителя  записать сумму
записать сумму  ;
3) неопределённые коэффициенты в числителях простейших дробей
;
3) неопределённые коэффициенты в числителях простейших дробей  найти из условия тождественного равенства исходной дроби и записанной суммы простейших дробей.
найти из условия тождественного равенства исходной дроби и записанной суммы простейших дробей.








 ;
;







 — верно.
— верно.



