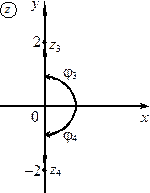Модуль, аргумент и тригонометрическая форма комплексного числаМодулем комплексного числа
Геометрически модуль комплексного числа — это длина радиус-вектора, изображающего число z, или полярный радиус точки (x; y), (рис. 79).
Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x; y)). Обозначение Формула для вычисления аргумента комплексного числа имеет вид
Замечание (к определению аргумента комплексного числа) Значение
Так как геометрически очевидно (рис. 79), что
Запись z = x + iy называется алгебраической формой комплексного числа z; запись z = r (cos j + i sin j) называется тригонометрической формой комплексного числа z, при этом Примеры (геометрическое изображение и тригонометрическая форма комплексных чисел) Изобразим на комплексной плоскости следующие числа и запишем их в тригонометрической форме:
|
называется неотрицательное действительное число r, вычисляемое по формуле
. (1)
,причем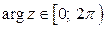 
или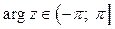 
, (рис. 79).
Аргумент комплексного числа, (2)
причем, при определении угла 
по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z:
, называют главным значением аргумента комплексного числа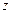 
; при этом значения всех возможных углов 
обозначают 
; очевидно, что 
, 
.
и 
, то
Тригонометрическая форма комплексного числа. (3)
.
, 
Þ 
Þ 
;
Þ 
, 
Þ 
Þ 
;
Þ 
, 
Þ
Þ
;
, 
;
, 
;
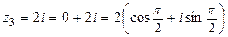6) 
, то есть для z = 0 будет 
, j не определен.
