Основные элементарные, элементарные и неэлементарные функции
Аналитически заданные функции, записанные в явной форме, принято разделять на основные элементарные функции, элементарные функции и неэлементарные функции. Основными элементарными функциями называются следующие функции: постоянная функция степенная функция показательная функция логарифмическая функция тригонометрические функции обратные тригонометрические функции гиперболические функции Большинство этих функций изучались в элементарной математике. Их определения, основные свойства и графики нужно знать на память. Повторению этих функций, а также определению гиперболических функций посвящен §10 изучаемой темы. Элементарной функцией называется функция, которая записывается одной формулой вида Например, к элементарным относятся следующие функции: Неэлементарной функцией называется функция, которая не относится к элементарным; например, если она не записывается одной формулой или содержит бесконечное число арифметических операций. Например, нелементарным являются следующие функции: 1) 2) функция Дирихле: 3)
|
;
;
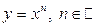, где a > 0, a ¹ 1;
, где a > 0, a ¹ 1;
;
, 
;
.
, где справа стоящее выражение 
составлено из основных элементарных функций и чисел при помощи конечного числа операций сложения, вычитания, умножения, деления и суперпозиции функций.
; 
; 
; 
.
.
