1. 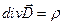
|  - теорема Гаусса, являющаяся
обобщением закона Кулона; q - полный свободный заряд в объеме V. - теорема Гаусса, являющаяся
обобщением закона Кулона; q - полный свободный заряд в объеме V.
|
2. 
|  - закон полного тока;
J – полный ток, охватываемый контуром L,
S – поверхность, натянутая на контур L. - закон полного тока;
J – полный ток, охватываемый контуром L,
S – поверхность, натянутая на контур L.
|
3. 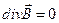
|  - замкнутость линий индукции магнитного поля (отсутствие магнитных зарядов) - замкнутость линий индукции магнитного поля (отсутствие магнитных зарядов)
|
4. 
| ei =  - закон электромагнитной индукции - закон электромагнитной индукции
|
Уравнения Максвелла дополняются материальными соотношениями (4), (5) и (6).
На границе раздела двух сред выполняются следующие граничные условия для нормальных и тангенциальных составляющих векторов напряженности и индукции полей:

 (7)
(7)
(s - поверхностная плотность свободных зарядов);
 ,
,  (8)
(8)
(i – линейная поверхностная плотность тока свободных зарядов, протекающего вдоль границы перпендикулярно Ht2 и Ht1).
Закон сохранения энергии электромагнитного поля выражается уравнением:
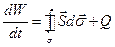 , (9)
, (9)
где W – энергия поля в объеме V,  - поток энергии через поверхность s, ограничивающую объем V, Q – количество теплоты, выделяющееся в объеме V, а
- поток энергии через поверхность s, ограничивающую объем V, Q – количество теплоты, выделяющееся в объеме V, а  - вектор плотности потока энергии (вектор Умова-Пойнтинга). В дифференциальной форме (9) имеет вид уравнения непрерывности:
- вектор плотности потока энергии (вектор Умова-Пойнтинга). В дифференциальной форме (9) имеет вид уравнения непрерывности:
 , (10)
, (10)
где  - плотность энергии электромагнитного поля,
- плотность энергии электромагнитного поля,
 ,
,
 - джоулево тепло, выделяющееся в единице объема.
- джоулево тепло, выделяющееся в единице объема.
ЭЛЕКТРОСТАТИКА

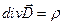
 - теорема Гаусса, являющаяся
обобщением закона Кулона; q - полный свободный заряд в объеме V.
- теорема Гаусса, являющаяся
обобщением закона Кулона; q - полный свободный заряд в объеме V.

 - закон полного тока;
J – полный ток, охватываемый контуром L,
S – поверхность, натянутая на контур L.
- закон полного тока;
J – полный ток, охватываемый контуром L,
S – поверхность, натянутая на контур L.
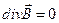
 - замкнутость линий индукции магнитного поля (отсутствие магнитных зарядов)
- замкнутость линий индукции магнитного поля (отсутствие магнитных зарядов)

 - закон электромагнитной индукции
- закон электромагнитной индукции

 (7)
(7) ,
,  (8)
(8)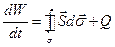 , (9)
, (9) - поток энергии через поверхность s, ограничивающую объем V, Q – количество теплоты, выделяющееся в объеме V, а
- поток энергии через поверхность s, ограничивающую объем V, Q – количество теплоты, выделяющееся в объеме V, а  - вектор плотности потока энергии (вектор Умова-Пойнтинга). В дифференциальной форме (9) имеет вид уравнения непрерывности:
- вектор плотности потока энергии (вектор Умова-Пойнтинга). В дифференциальной форме (9) имеет вид уравнения непрерывности: , (10)
, (10) - плотность энергии электромагнитного поля,
- плотность энергии электромагнитного поля, ,
, - джоулево тепло, выделяющееся в единице объема.
- джоулево тепло, выделяющееся в единице объема.


