Краткие теоретические сведения. Электростатика – раздел электродинамики, в котором рассматриваются не зависящие от времени поля распределения неподвижных зарядов ( )
Электростатика – раздел электродинамики, в котором рассматриваются не зависящие от времени поля распределения неподвижных зарядов (
Из (1.2) следует, что электрическое поле системы неподвижных зарядов носит потенциальный характер, т.е.
где j - потенциал электростатического поля. Потенциал j определен с точностью до постоянной, значение которой обусловлено выбором точки нулевого потенциала:
Т.к. сила, действующая на пробный заряд q, помещенный в рассматриваемую точку поля,
Подстановка (1.3) в (1.1) позволяет объединить уравнения (1.1) и (1.2) в одно основное уравнение электростатики:
В области пространства, где заряды отсутствуют, уравнение (1.6), называемое уравнением Пуассона, переходит в уравнение Лапласа:
Основной задачей электростатики является нахождение поля заданного распределения заряда и сил, действующих на заряд, помещенный в рассматриваемую точку поля. Такая задача в общем случае сводится к решению уравнения (1.6) или (1.7) с последующим определением вектора напряженности в соответствии с (1.3). При решении уравнений (1.6) и (1.7) следует помнить, что потенциал непрерывен на границах разделов сред, а производные потенциала, определяющие проекции напряженности электрического поля, изменяются в соответствии с граничными условиями (7). Во многих случаях решение основной задачи электростатики может быть более простым при использовании принципа суперпозиции для напряженностей или потенциалов. Так, поле точечного заряда определяется следующими выражениями:
если начало координат совмещено с зарядом, или
(здесь Рассматривая в системе объемно распределенных зарядов элементарный заряд dq=rdV¢; как точечный,его поле можно записать в виде (см. рис 1.1):
где Тогда напряженность и потенциал электростатического поля всей системы равны:
Если система зарядов обладает центральной или осевой симметрией и, кроме того, существуют поверхности, на которых значение напряженности остается постоянным, наиболее рациональным для расчета поля является использование теоремы Гаусса в интегральной форме
Энергия электростатического поля в общем случае равна
где интегрирование ведется по всей области, занятой полем. Если объемно распределенный заряд ограничен в пространстве, то его энергия, равная энергии поля, определяется выражением:
причем в последнем интеграле интегрирование ведется по области, занятой зарядом. Если система объемно распределенных зарядов помещена во внешнее электростатическое поле, то полная энергия системы W = W1 + W2 + W12, где W1 и W2 – собственная энергия системы зарядов и внешнего поля, определяемые выражениями (1.13), (1.14), а W12 – энергия взаимодействия зарядов и поля, равная
Здесь Для системы точечных зарядов энергия взаимодействия
где jik – потенциал поля k -го заряда в точке расположения i -го заряда; ji - потенциал, создаваемый всеми зарядами системы кроме i -го в точке расположения этого заряда. С учетом (1.9) энергия взаимодействия системы точечных зарядов принимает вид:
При этом сила, действующая на i -ый заряд, определяется общим выражением:
(индекс i указывает на то, что градиент берется по координатам i -го заряда). На больших расстояниях от системы зарядов с линейным размером l (r >>r¢, l; начало отсчета совмещается с какой-либо точкой системы, чаще всего – с центром масс) потенциал можно представить в виде суммы мультипольных потенциалов
получаемых разложением в (1.11) подынтегральной функции 1/R в ряд по степеням малости r¢. Первые два слагаемые в (1.19)имеют вид:
Выражение (1.20) описывает поле точечного заряда, равного полному заряду системы и расположенного в начале координат, а выражение (1.21) определяет дипольный потенциал – поле системы, электрический дипольный момент которой равен:
Потенциал j2 называется квадрупольным, j3 – октупольным и т.д. Важно отметить, что
В общем случае потенциал системы зарядов на большом расстоянии от нее определяется первым не равным нулю мультипольным потенциалом. Особую роль играет поле диполя – как правило, реальные системы зарядов в целом электронейтральны, и их поле определяется дипольным моментом. Потенциалу ji соответствует напряженность электрического поля диполя
Электрический диполь Электростатическое поле в веществе принципиально зависит от структуры вещества – наличия или отсутствия свободных зарядов. Вещество, в котором свободные заряды отсутствуют, является диэлектриком. Существование в диэлектрике связанных зарядов (электронов и ядер в атомах и молекулах, которые под действием электрического поля могут смещаться лишь на микроскопические расстояния) приводит к его поляризации. Количественной характеристикой степени поляризации служит вектор поляризации
В однородной и изотропной среде и в слабых полях вектор поляризации пропорционален напряженности электрического поля:
где k - диэлектрическая восприимчивость. Объединение (1.24) и (1.25) приводит к материальному уравнению
На границе раздела двух диэлектриков граничные условия
дополняются граничным условием для вектора поляризации
где s¢; - поверхностная плотность связанных зарядов. В отличие от диэлектриков, в проводниках существуют свободные заряды, которые под действием поля могут перемещаться на макроскопические расстояния и полностью экранировать электростатическое поле. Макроскопической характеристикой способности свободных зарядов перемещаться является электропроводность g, связанная с напряженностью электрического поля законом Ома (5). Т.к. электростатическое поле связано с неподвижными зарядами (
где Энергия проводника, заряженного зарядом q до потенциала j, равна:
Энергия системы заряженных проводников может быть представлена в виде:
Здесь jk – потенциал, создаваемый всеми проводниками системы на k -том проводнике. Потенциал i -го заряда системы заряженных проводников является линейной функцией зарядов проводников:
Коэффициенты aik = aki зависят от взаимного расположения, формы и геометрических размеров проводников, а также от диэлектрической проницаемости окружающей среды и называются потенциальными коэффициентами. Соответственно, заряды проводников также являются линейными функциями их потенциалов, т.е.:
Величины Сik называются емкостными коэффициентами, причем матрица коэффициентов Cik является обратной матрице коэффициентов aik. Коэффициенты Cii > 0 (собственные емкости), Cik = Cki < 0 (коэффициенты взаимной емкости). Для уединенного проводника
На заряженный проводник или незаряженный, но помещенный во внешнее электрическое поле, со стороны поля действуют силы, растягивающие этот проводник. Сила, действующая на единицу поверхности, перпендикулярна этой поверхности и равна
|

 ). При этом система уравнений Максвелла сводится к двум уравнениям:
). При этом система уравнений Максвелла сводится к двум уравнениям: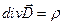 (1.1)
(1.1) . (1.2)
. (1.2) , (1.3)
, (1.3) . (1.4)
. (1.4) , то работа электростатического поля по перемещению заряда из точки 1 поля в точку 2 равна:
, то работа электростатического поля по перемещению заряда из точки 1 поля в точку 2 равна: . (1.5)
. (1.5) . (1.6)
. (1.6) . (1.7)
. (1.7) ,
,  , (1.8)
, (1.8) ,
,  (1.9)
(1.9) - радиус-вектор точки наблюдения поля, а
- радиус-вектор точки наблюдения поля, а  - радиус-вектор заряда).
- радиус-вектор заряда).
 ,
, ,
, .
. , (1.10)
, (1.10) . (1.11)
. (1.11) . (1.12)
. (1.12) , (1.13)
, (1.13) , (1.14)
, (1.14) . (1.15)
. (1.15) - плотность заряда системы а j2 (r ¢) – потенциал внешнего поля в области, занятой зарядом.
- плотность заряда системы а j2 (r ¢) – потенциал внешнего поля в области, занятой зарядом. , (1.16)
, (1.16) . (1.17)
. (1.17) (1.18)
(1.18) , (1.19)
, (1.19) , (1.20)
, (1.20) . (1.21)
. (1.21) . (1.22)
. (1.22) и т.д.
и т.д. . (1.23)
. (1.23) во внешнем электрическое поле напряженностью
во внешнем электрическое поле напряженностью  обладает энергией
обладает энергией  ; при этом на него действует сила
; при этом на него действует сила  и момент силы
и момент силы  .
. - электрический дипольный момент единицы объема диэлектрика. Связь между вектором напряженности электрического поля в диэлектрике
- электрический дипольный момент единицы объема диэлектрика. Связь между вектором напряженности электрического поля в диэлектрике  индукцией электрического поля
индукцией электрического поля  и вектором поляризации
и вектором поляризации  . (1.24)
. (1.24) , (1.25)
, (1.25) . (1.26)
. (1.26)
 , (1.27)
, (1.27) ) и g ¹ 0, то в проводниках электростатическое поле отсутствует. Кроме того, из уравнения
) и g ¹ 0, то в проводниках электростатическое поле отсутствует. Кроме того, из уравнения  следует, что в проводниках отсутствуют и объемные заряды. Другими словами, вне зависимости от того, заряжен проводник или не заряжен, но помещен в электростатическое поле, в его объеме заряды отсутствуют – сообщенный или наведенный заряды распределяются по поверхности. При этом весь объем и поверхность проводника эквипотенциальны. Вблизи поверхности проводника напряженность электрического поля перпендикулярна его поверхности:
следует, что в проводниках отсутствуют и объемные заряды. Другими словами, вне зависимости от того, заряжен проводник или не заряжен, но помещен в электростатическое поле, в его объеме заряды отсутствуют – сообщенный или наведенный заряды распределяются по поверхности. При этом весь объем и поверхность проводника эквипотенциальны. Вблизи поверхности проводника напряженность электрического поля перпендикулярна его поверхности: , (1.28)
, (1.28) - внешняя нормаль к поверхности проводника, s - поверхностная плотность заряда, а e - диэлектрическая проницаемость окружающей среды.
- внешняя нормаль к поверхности проводника, s - поверхностная плотность заряда, а e - диэлектрическая проницаемость окружающей среды. . (1.29)
. (1.29) . (1.30)
. (1.30) , (1.31)
, (1.31) . (1.32)
. (1.32) , для системы из двух проводников (конденсатора), заряженных одинаковыми по величине и противоположными по знаку зарядами q, величина
, для системы из двух проводников (конденсатора), заряженных одинаковыми по величине и противоположными по знаку зарядами q, величина  называется емкостью конденсатора (U – напряжение на конденсаторе). Введение емкостных коэффициентов позволяет записать выражение для энергии системы проводников в виде:
называется емкостью конденсатора (U – напряжение на конденсаторе). Введение емкостных коэффициентов позволяет записать выражение для энергии системы проводников в виде: . (1.33)
. (1.33)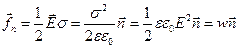 . (1.33)
. (1.33)


