Примеры решения задач. Пример 1.Тонкий диск радиуса а равномерно заряжен м поверхностной плотностью зарядаs
Пример 1. Тонкий диск радиуса а равномерно заряжен м поверхностной плотностью зарядаs. Определить напряженность электрического поля на оси симметрии диска. Диэлектрическую проницаемость среды принять равной 1.
где Учтем, что при наложении полей всех элементарных зарядов радиальные составляющие компенсируются. Поэтому результирующее поле в точке А будет направлено вдоль оси Oz, т.е. Ez = E. Тогда
и Из полученного выражения видно, что в центре диска (z = 0) Рассмотренная задача может быть решена и с использованием принципа суперпозиции для потенциалов. Так, потенциал, создаваемый элементарным зарядом dq в точке наблюдения А Выполняя интегрирование по поверхности диска, получаем:
Учтем, что j зависит только от z, и что
Пример 2. Определить напряженность электрического поля на оси симметрии тонкого заряженного с поверхностной плотностью заряда s диска, если в его центре имеется круглое отверстие. Радиус диска а, радиус отверстия b < a. Задача сводится к предыдущей. Отличие заключается лишь в том, что меняется нижний предел интегрирования:
Этот результат может быть получен иным способом, если использовать, как известное, значение напряженности электрического поля на оси сплошного тонкого диска. Поле диска с отверстием можно рассматривать как результат наложения полей двух дисков - одного (радиуса а) с поверхностной плотностью заряда s, и соосного с ним другого (радиуса b), заряженного с поверхностной плотностью заряда - s. Тогда
Пример 3. Определить потенциал электрического поля на окружности тонкого кольца радиуса а, равномерно заряженного с линейной плотностью заряда t. Диэлектрическая проницаемость среды равна 1. Т.к. потенциал – величина скалярная и зависит только от расстояния между зарядом и точкой наблюдения, то для решения задачи удобно совместить начало координат О с точкой наблюдения (см. рис1.5). Для выбранной геометрии задачи
Из рис 1.5 видно, что полярный угол f принимает значения от 0 до p. Поэтому
Пример 4. Сфера радиуса R заряжена с поверхностной плотностью заряда s=s0×;cos q, где q - азимутальный угол. Определить напряженность электрического поля на расстоянии r >> R вдоль оси дипольного момента сферы, а также в плоскости, перпендикулярной оси диполя и пересекающей его центр.
перпендикулярные оси Oz, при наложении компенсируются, то полный дипольный момент сферы p = pz. Из рис.1.6 видно, что
Тогда полный дипольный момент сферы
На большом расстоянии от системы зарядов
Следовательно, в направлении оси Oz
В плоскости z = 0 дипольный момент сферы перпендикулярен радиус-вектору
|

 Как видно из рис. 1.4, напряженность электрического поля, создаваемого элементарным зарядом
Как видно из рис. 1.4, напряженность электрического поля, создаваемого элементарным зарядом 
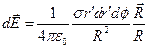 ,
, .
. ,
, .
. . Если а ® ¥, то поле становится однородным и его напряженность совпадает с напряженностью поля заряженной бесконечной плоскости.
. Если а ® ¥, то поле становится однородным и его напряженность совпадает с напряженностью поля заряженной бесконечной плоскости. .
. .
. . Тогда получаем
. Тогда получаем .
. .
. .
.
 .
. .
.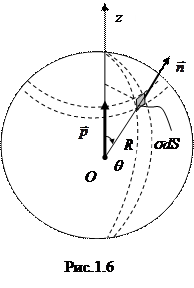 Т.к. составляющие элементарного дипольного момента
Т.к. составляющие элементарного дипольного момента ,
, .
. .
.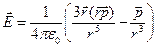 .
.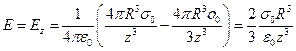 .
. . Поэтому
. Поэтому , и напряженность электрического поля, по-прежнему направленная вдоль оси Oz, определяется выражением
, и напряженность электрического поля, по-прежнему направленная вдоль оси Oz, определяется выражением  .
.


