Примеры решения задач. Пример 1.Незаряженная проводящая сфера радиуса R помещена во внешнее однородное электрическое поле.
Пример 1. Незаряженная проводящая сфера радиуса R помещена во внешнее однородное электрическое поле., в результате чего на ее поверхности появляется индуцированный заряд, плотность которого s = s0cosq, где s0 = const и q - азимутальный угол. Определить силы, действующие на сферу со стороны электрического поля.
Как видно из рис.1.7б), при наложении всех элементарных сил, действующих на положительно (отрицательно) заря-женную полусферу, составляющие, перпендикулярные оси Oz, компенсируются. Результирующая сила, действующая на полусферу, обеспечивается вкладами
Тогда Такая же по величине и противоположная по направлению сила действует и на отрицательно заряженную часть сферы. Таким образом, на сферу действуют силы, растягивающие ее вдоль линий напряженности внешнего поля.
Пример 2. Точечный заряд q находится на расстоянии d от центра заземленной сферы радиуса R. Определить потенциал электростатического поля системы.
Пусть в рассматриваемом примере заряд-изображение q¢; находится на расстоянии х от центра сферы О (см. рис.1.8). Значения величин х и q¢; должны быть такими, чтобы поверхность сферы R = const была эквипотенциальной поверхностью j = 0 для поля системы зарядов q и q¢; в области пространства вне сферы. Из рис 1.8. видно, что для точек В и N можно записать условие равенства потенциалов нулю в виде двух уравнений:
Решая совместно эти уравнения, получаем:
Тогда в соответствии с принципом суперпозиции потенциал в точке наблюдения Р
Если ввести полярный угол q, то из треугольника MCP видно, что
Пример 3. Четыре одинаковые проводящие маленькие сферы расположены по углам квадрата. Сфера 1 несет заряд q. Затем она соединяется тонкой проволокой поочередно со сферами 2, 3 и 4 (нумерация циклическая). Найти распределение заряда между проводниками по окончании всех операций. Потенциальные коэффициенты системы заданы.
и учтем, что при последовательном соединении сфер заряд перетекает до выравнивания потенциалов в каждой из операций. Учтем также, что в рассматриваемой системе имеют место лишь два отличающихся относительных расположения зарядов - 12, 23, 34, 41 и 13, 24. Поэтому
В этих соотношениях Первое соединение 1-2 (рис.1.9б)).
Приравнивая эти потенциалы, получаем Второе соединение 1-3 (рис.1.9в))
Приравнивая Третье соединение 1-4 (рис.1.9г)).
Приравнивая правые части этих уравнений и учитывая, что
|

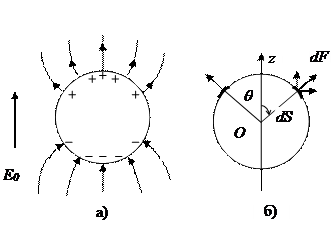 На рис 1.7а) схематически показано распределение индуцированного заряда по поверхности проводящей сферы при помещении ее во внешнее однородное электростатическое поле. В соответствии с формулой (1.33) на элемент поверхности dS = R2 sinqdqdf действует сила
На рис 1.7а) схематически показано распределение индуцированного заряда по поверхности проводящей сферы при помещении ее во внешнее однородное электростатическое поле. В соответствии с формулой (1.33) на элемент поверхности dS = R2 sinqdqdf действует сила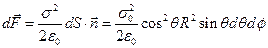 .
.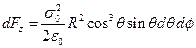 .
.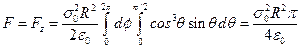 .
. Одним из наиболее эффективных методов определения поля системы точечных зарядов при наличии проводников является метод изображений. Этот метод заключается в введении системы определенным образом подобранных зарядов-изображений, которые расположены так, что действие этих зарядов обеспечивает требуемые граничные условия. При этом заряды-изображения должны находиться вне области существования искомого поля.
Одним из наиболее эффективных методов определения поля системы точечных зарядов при наличии проводников является метод изображений. Этот метод заключается в введении системы определенным образом подобранных зарядов-изображений, которые расположены так, что действие этих зарядов обеспечивает требуемые граничные условия. При этом заряды-изображения должны находиться вне области существования искомого поля.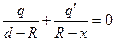 - для точки B,
- для точки B,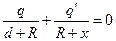 - для точки N.
- для точки N.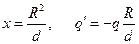 .
.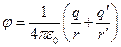 .
.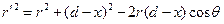 .
. При решении задачи воспользуемся выражением (1.31):
При решении задачи воспользуемся выражением (1.31):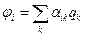
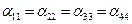 ,
,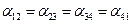 .
.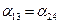 .
.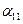 - собственный потенциальный коэффициент (для первой сферы в начальный момент
- собственный потенциальный коэффициент (для первой сферы в начальный момент 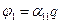 , потенциалы остальных сфер нулевые – рис.1.9а));
, потенциалы остальных сфер нулевые – рис.1.9а)); 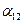 учитывает влияние зарядов сфер на соседние сферы вдоль стороны квадрата, а
учитывает влияние зарядов сфер на соседние сферы вдоль стороны квадрата, а 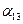 - влияние на сферы вдоль диагонали. С учетом введенных обозначений и сделанных замечаний рассмотрим последовательные соединения.
- влияние на сферы вдоль диагонали. С учетом введенных обозначений и сделанных замечаний рассмотрим последовательные соединения.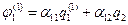 ,
,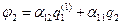 .
.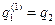 . Кроме того,
. Кроме того, 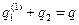 . Следовательно,
. Следовательно, 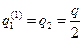 .
.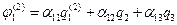 ,
,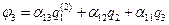 .
.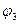 и
и  , а также учитывая, что
, а также учитывая, что 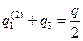 , получаем
, получаем 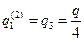 .
.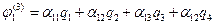 ,
,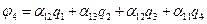 .
.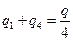 , получаем окончательное распределение зарядов на сферах:
, получаем окончательное распределение зарядов на сферах: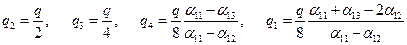 .
.


