ТОК СМЕЩЕНИЯ. ВТОРОЕ УРАВНЕНИЕ МАКСВЕЛЛА
Если электромагнитное поле стационарно, то ротор вектора
Вектор
При этом дивергенция
Проведем круговой контур Г, охватывающий провод, по которому течет ток к конденсатору (рис.5.1). Обозначим через
где Для поверхности
Этот результат является заведомо неверным, т.к. и поверхность Таким образом, в случае изменяющихся во времени полей уравнение (5.3) несправедливо. Поэтому можно сказать, что в уравнении (5.3) не хватает одного слагаемого, которое зависит от производных полей по времени. Для стационарных полей это слагаемое равно нулю. Для согласования уравнений (5.3) и (5.4) Максвелл ввел слагаемое, которое имеет размерность плотности тока, и назвал его плотностью тока смещения. С учетом этого слагаемого для ротора вектора
Сумма плотности тока проводимости и плотности тока смещения называется плотностью полного тока:
Можно показать, что дивергенция тока смещения равна:
По теореме Гаусса
поменяем местами порядок дифференцирования по времени и координатам, получаем:
Подставим (5.6) в формулу (5.5): Тогда для ротора вектора
Это второе уравнение Максвелла. Из него следует, что меняющееся во времени электрическое поле Термин «ток смещения» является чисто условным. Это изменяющееся во времени электрическое поле. Ток смещения обладает только одним физическим свойством – способностью создавать магнитное поле. Токи смещения не сопровождаются выделением ленц-джоулева тепла. Ток смещения есть везде, где есть меняющееся во времени электрическое поле. Внутри проводов, по которым течет переменный электрический ток, ток смещения также существует, но он пренебрежительно мал по сравнению с током проводимости. Учет токов смещения приводит к тому, что цепи непостоянных токов становятся замкнутыми, токи смещения проходят в тех участках, где нет проводников, например, между обкладками плоского конденсатора. Известно, что
В этом выражении Ток смещения сквозь произвольную поверхность S, очевидно, равен потоку вектора плотности тока смещения через эту поверхность:
В интегральной форме второе уравнение Максвелла имеет вид:
- циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру Г равна алгебраической сумме макротоков и токов смещения сквозь поверхность, натянутую на этот контур. Таким образом, электрическое и магнитное поля неразрывно связаны и могут взаимно порождать друг друга. Они образуют единое электромагнитное поле.
|

 в каждой точке поля равен плотности тока проводимости:
в каждой точке поля равен плотности тока проводимости: . (5.3)
. (5.3) связан с плотностью заряда в той же точке уравнением непрерывности:
связан с плотностью заряда в той же точке уравнением непрерывности: . (5.4)
. (5.4) Рассмотрим теперь изменяющееся во времени поле. Пусть магнитное поле создается током, текущим при зарядке конденсатора от источника постоянного напряжение U (рис.5.1). Этот ток меняется во времени и при напряжении на конденсатора, равном U, прекращается. Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора.
Рассмотрим теперь изменяющееся во времени поле. Пусть магнитное поле создается током, текущим при зарядке конденсатора от источника постоянного напряжение U (рис.5.1). Этот ток меняется во времени и при напряжении на конденсатора, равном U, прекращается. Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора. поверхность, пересекающую провод и ограниченную контуром Г. Тогда по Закону полного тока
поверхность, пересекающую провод и ограниченную контуром Г. Тогда по Закону полного тока ,
, - сила тока, заряжающего конденсатор.
- сила тока, заряжающего конденсатор. , не пересекающей провод с током (рис.5. 1), имеем:
, не пересекающей провод с током (рис.5. 1), имеем: .
. (рис.5.1). Циркуляция вектора
(рис.5.1). Циркуляция вектора  .
. .
. . (5.5)
. (5.5) , продифференцировав это выражение по времени, имеем:
, продифференцировав это выражение по времени, имеем: ,
,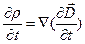 . (5.6)
. (5.6) , и
, и 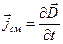 .
. . (5.7)
. (5.7) порождает магнитное поле
порождает магнитное поле  , где
, где  – вектор поляризации. Тогда плотность тока смещения в диэлектрике
– вектор поляризации. Тогда плотность тока смещения в диэлектрике .
.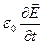 определяет плотность тока смещения в вакууме,
определяет плотность тока смещения в вакууме, 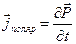 называется плотностью тока поляризации. Он представляет собой плотность тока, обусловленного упорядоченным перемещением связанных зарядов в диэлектрике при изменении его поляризации. Это смещение зарядов в молекулах неполярного диэлектрика или поворот молекул – диполей в полярных диэлектриках.
называется плотностью тока поляризации. Он представляет собой плотность тока, обусловленного упорядоченным перемещением связанных зарядов в диэлектрике при изменении его поляризации. Это смещение зарядов в молекулах неполярного диэлектрика или поворот молекул – диполей в полярных диэлектриках. .
.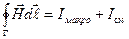 ,
,


