
Возьмем два контура 1 и 2, расположенные близко друг к другу в неферромагнитной среде (рис.4.6). Если в контуре 1 течет ток силы  , он создает через контур 2 пропорциональный
, он создает через контур 2 пропорциональный  полный
полный
магнитный поток  . При изменениях тока
. При изменениях тока  в контуре 2 индуцируется ЭДС
в контуре 2 индуцируется ЭДС
 .
.
Аналогично, при протекании в контуре 2 тока силы  возникает сцепленный с контуром 1 поток
возникает сцепленный с контуром 1 поток
 .
.
При изменениях тока  в контуре 1 индуктируется ЭДС
в контуре 1 индуктируется ЭДС 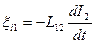 .
.
Контуры 1 и 2 называют связанными, а явление возникновения ЭДС в одном из контуров при изменении силы тока в другом – взаимной индукцией. Коэффициенты пропорциональности  и
и  называют взаимной индуктивностью контуров. В отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу:
называют взаимной индуктивностью контуров. В отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу:
 .
.
 Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости среды, окружающей контуры. Измеряется
Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости среды, окружающей контуры. Измеряется  в тех же единицах, что и L (в Генри).
в тех же единицах, что и L (в Генри).
Найдем взаимную индуктивность двух катушек, намотанных на общий тороидальный железный сердечник (рис.4.7). Линии магнитной индукции сосредотачиваются внутри сердечника, поэтому можно считать, что возбуждаемое любой из обмоток магнитное поле будет иметь всюду в сердечнике одинаковую напряженность. Если первая обмотка имеет  витков, и по ней течёт ток силы
витков, и по ней течёт ток силы  витков, то согласно теореме о циркуляции
витков, то согласно теореме о циркуляции  , или
, или  ,
,
где  – длина сердечника.
– длина сердечника.
Магнитный поток через поперечное сечение сердечника  , где S – площадь поперечного сечения сердечника. Подставив
, где S – площадь поперечного сечения сердечника. Подставив  , получаем
, получаем  . Это выражение умножим на число витков второй обмотки
. Это выражение умножим на число витков второй обмотки 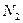 , получим полный поток, сцепленный со второй обмоткой:
, получим полный поток, сцепленный со второй обмоткой:
 .
.
Сравнивая это выражение с выражением (4.1), получаем
 .
.
Аналогично можно получить  .
.
В общем случае  , так как множитель
, так как множитель  (магнитная проницаемость среды), входящий в эти выражения, зависит от напряженности поля
(магнитная проницаемость среды), входящий в эти выражения, зависит от напряженности поля  в сердечнике. Если
в сердечнике. Если  , то один и тот же ток, пропускаемый один раз по первой, а второй раз - по второй катушке, создает в сердечнике поле разной напряженности
, то один и тот же ток, пропускаемый один раз по первой, а второй раз - по второй катушке, создает в сердечнике поле разной напряженности  . Соответственно, значения
. Соответственно, значения  в обоих случаях будут различны, так что при
в обоих случаях будут различны, так что при  значения
значения  и
и  не совпадают. Если сердечник неферромагнитный, например, деревянный, то
не совпадают. Если сердечник неферромагнитный, например, деревянный, то  , т.к.
, т.к.  не зависит от
не зависит от  .
.
4.6.ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ОБЪЕМНАЯ ПЛОТНОСТЬ ЭНЕРГИИ МАГНИТНОГО ПОЛЯ В ВЕЩЕСТВЕ
 Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде. В соленоиде течет ток
Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде. В соленоиде течет ток  , который образует магнитный поток, сцепленный с соленоидом. Если отключить соленоид от источника и замкнуть его на сопротивление
, который образует магнитный поток, сцепленный с соленоидом. Если отключить соленоид от источника и замкнуть его на сопротивление  , по цепи пойдет постепенно убывающий ток. Работа, совершаемая этим током за время
, по цепи пойдет постепенно убывающий ток. Работа, совершаемая этим током за время  равна
равна
 .
.
Если индуктивность соленоида остается постоянной,  , то
, то 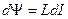 , и
, и
 . (4.3)
. (4.3)
Эта работа идет на нагревание проводников. Вследствие совершения этой работы происходит исчезновение магнитного поля, и так как никаких изменений в окружающей цепь среде не происходит, следует заключить, что работа совершается за счет энергии магнитного поля, а выражения (4.3) как раз и определяет эту работу. Вся работа, произведенная током при убывании магнитного поля до нуля равна
 ,
,
и энергия магнитного поля  .
.
Объемной плотностью энергии  магнитного поля называется энергия этого поля, отнесенная к его объему:
магнитного поля называется энергия этого поля, отнесенная к его объему:
 .
.
Однако  (поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем
(поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем  , где
, где  - длина соленоида,
- длина соленоида, 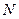 - число витков соленоида, тогда
- число витков соленоида, тогда
 .
.
Энергия  , локализованная во всем объеме магнитного поля равна:
, локализованная во всем объеме магнитного поля равна:
 .
.
Если поле в данной точке пространства создано несколькими контурами с током, то энергия результирующего магнитного поля равна:
 ,
,
где  - сила тока в
- сила тока в  -том контуре,
-том контуре,  - потокосцепление
- потокосцепление  - того контура, равное сумме потокосцепления самоиндукции (магнитного потока самоиндукции)
- того контура, равное сумме потокосцепления самоиндукции (магнитного потока самоиндукции)  - того контура и магнитного потока взаимоиндукции
- того контура и магнитного потока взаимоиндукции  -того контура с остальными,
-того контура с остальными,  . Поэтому энергия магнитного поля равна
. Поэтому энергия магнитного поля равна
 ,
,
 – взаимная индуктивность
– взаимная индуктивность  -того и i - того контуров с токами
-того и i - того контуров с токами  и
и  .
.


 , он создает через контур 2 пропорциональный
, он создает через контур 2 пропорциональный  . При изменениях тока
. При изменениях тока  .
. возникает сцепленный с контуром 1 поток
возникает сцепленный с контуром 1 поток .
.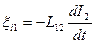 .
. и
и  называют взаимной индуктивностью контуров. В отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу:
называют взаимной индуктивностью контуров. В отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу: .
. Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости среды, окружающей контуры. Измеряется
Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости среды, окружающей контуры. Измеряется  витков, и по ней течёт ток силы
витков, и по ней течёт ток силы  , или
, или  ,
, – длина сердечника.
– длина сердечника. , где S – площадь поперечного сечения сердечника. Подставив
, где S – площадь поперечного сечения сердечника. Подставив  , получаем
, получаем  . Это выражение умножим на число витков второй обмотки
. Это выражение умножим на число витков второй обмотки 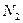 , получим полный поток, сцепленный со второй обмоткой:
, получим полный поток, сцепленный со второй обмоткой: .
. .
. .
. , так как множитель
, так как множитель  (магнитная проницаемость среды), входящий в эти выражения, зависит от напряженности поля
(магнитная проницаемость среды), входящий в эти выражения, зависит от напряженности поля  в сердечнике. Если
в сердечнике. Если  , то один и тот же ток, пропускаемый один раз по первой, а второй раз - по второй катушке, создает в сердечнике поле разной напряженности
, то один и тот же ток, пропускаемый один раз по первой, а второй раз - по второй катушке, создает в сердечнике поле разной напряженности  значения
значения  Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде. В соленоиде течет ток
Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде. В соленоиде течет ток  , который образует магнитный поток, сцепленный с соленоидом. Если отключить соленоид от источника и замкнуть его на сопротивление
, который образует магнитный поток, сцепленный с соленоидом. Если отключить соленоид от источника и замкнуть его на сопротивление  , по цепи пойдет постепенно убывающий ток. Работа, совершаемая этим током за время
, по цепи пойдет постепенно убывающий ток. Работа, совершаемая этим током за время  равна
равна .
. , то
, то 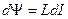 , и
, и . (4.3)
. (4.3) ,
, .
. магнитного поля называется энергия этого поля, отнесенная к его объему:
магнитного поля называется энергия этого поля, отнесенная к его объему: .
. (поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем
(поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем  , где
, где 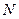 - число витков соленоида, тогда
- число витков соленоида, тогда .
. , локализованная во всем объеме магнитного поля равна:
, локализованная во всем объеме магнитного поля равна: .
. ,
, - сила тока в
- сила тока в  -том контуре,
-том контуре,  - потокосцепление
- потокосцепление  . Поэтому энергия магнитного поля равна
. Поэтому энергия магнитного поля равна ,
, – взаимная индуктивность
– взаимная индуктивность  .
.


