Анализ сезонности. Коррелограмма
В общем виде периодическая зависимость может быть формально определена как корреляционная зависимость между каждым i-м и (i-n)-м элементом ряда, при этом n называют лагом (сдвигом, запаздыванием). Данную зависимость оценивает автокорреляционная функция АСF (Autocorrelation function), вычисляемая как последовательность корреляций между рядом и им же, сдвинутым на 1,2,…,n,… временных точек, лагов. АСF представляет собой коэффициенты автокорреляции, формула (5), для последовательности лагов из определенного диапазона, т.е. зависимость между разнесёнными по времени наблюдениями.
где М- математическое ожидание;
t и s – различные моменты времени, где t-s= n, (n – лаг);
Т.о. коэффициент автокорреляции при лаге 1 есть коэффициент корреляции между yt и yt-1. Если ряд стационарен, то данный коэффициент равняется коэффициенту корреляции между yt и yt-2; yt и yt-3 и т.д. Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы, которая представляет собой график зависимости значений автокорреляционной (АСF) или частной автокорреляционной (PАСF) функции от величины лага n (порядка коэффициента автокорреляции). Однако, если коррелированны yt и yt-1, а также yt-1 и yt-2, то и yt и yt-2 также коррелированны, т.е. корреляция при лаге 1 "вызывает" корреляцию при лаге 2, а, соответственно, и при больших лагах. Поэтому для исследования периодичности и получения более «чистой» картины периодических зависимостей используется PACF (Partial autocorrelation function), которая представляет собой «чистую» зависимость между наблюдениями. Частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами, например PACF при лаге 3 равняется корреляции рядов yt и yt-3, причем считается исключенной их корреляция с рядами yt-1 и yt-2. Т.о. PACF позволяет оценить порядок запаздывания процесса n для модели авторегрессии AR(n), которая будет рассмотрена ниже.
|

 , (5)
, (5) - среднеквадратическое отклонение
- среднеквадратическое отклонение  ;
; - среднее значение
- среднее значение 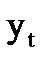 ;
; - автокорреляционная функция временного ряда
- автокорреляционная функция временного ряда 


