Спектральный (Фурье) анализ
Цель спектрального анализа - разложить комплексные стационарные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн, появление которых особенно существенно и значимо, формула (7). В результате анализа можно обнаружить всего несколько основных периодических компонент (функций синусов или косинусов) в изучаемом временном ряду, который, на первый взгляд, выглядит как случайный шум, что позволит изучить интересующее явление.
где а0 – константа; аi, bi – амплитуды соответствующих функций, коэффициенты регрессии, которые показывают степень, с которой соответствующие функции синусов и косинусов коррелируют с фактическими данными;
fi - частота Фурье или угловая частота, обратная периоду. i- номер соответствующих гармоник (косинуса и синуса) с определённым значением частоты; N- число наблюдений; q- для нечётного числа наблюдений q=(N-1)/2 - число различных синусов и косинусов, для чётного q=N/2 исуществует q значений косинусов и q-1 значений синусов. Для нахождения частот основных периодических составляющих (синусов и косинусов) временного ряда вычисляется периодограмма, формула (8), путём суммирования квадратов коэффициентов аi и bi для каждой частоты и умножения на N/2. Значения периодограммы на графике изображаются в зависимости от частот или периодов.
где I(fi) значение периодограммы на частоте fi; N - общая длина ряда. Сглаженная периодограмма, состоящая из усреднённых методом взвешенного или простого скользящего среднего значений периодограммы, представляет собой функцию спектральной плотности и используется для тех же целей. Одним из методов взвешенного скользящего среднего является метод Бартлетта (Bartlett). В интервале сглаживания, для каждой частоты, веса для взвешенного скользящего среднего значений периодограммы вычисляются как: wi = 1-(i/p) (для i = 0 до p); w-i = wi (для i
|


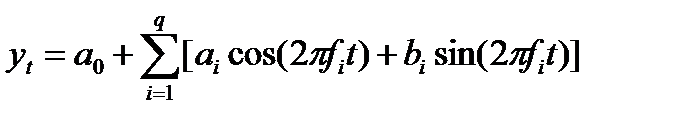 , (7)
, (7)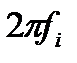 - круговая частота соответствующей функции, радиан.
- круговая частота соответствующей функции, радиан. (8)
(8) 0); p = (g-1)/2), где g- длина интервала сглаживания.
0); p = (g-1)/2), где g- длина интервала сглаживания.


