Построение главных компонент
Поскольку метод главных компонент основан на коррелированности исходных признаков, перед построением главных компонент необходимо проверить наличие корреляции между x1…xр для каждой составляющей устойчивого развития. Построим матрицу корреляций, используя соответствующие функции пакета Gretl. Коэффициенты линейной корреляции Пирсона рассчитываются при помощи команды главного меню View\Correlation Matrix. Выберем данный пункт меню (шаг 1.), в открывшемся окне при помощи кнопки Select выберем переменные x11…x71 (шаг 2.) и нажмём кнопку ОК (шаг 3.), как показано на рисунке 8.
Рисунок 8 – Определение коэффициентов корреляции x11…x71 Оценив коэффициенты корреляции, отражённые в появившемся окне (рисунок 9), отметим, что большинство признаков коррелированны между собой за исключением: Total assets (Совокупные активы)- Net Income (Чистая прибыль); Total assets (Совокупные активы)-Gross Cash (Валовая наличность); Total assets (Совокупные активы)- Cash Dividends (Наличные дивиденды); Shareholders return (Доход акционеров) - Net Income (Чистая прибыль); Shareholders return (Доход акционеров) - Gross Cash (Валовая наличность); Shareholders return (Доход акционеров) - Cash Dividends (Наличные дивиденды); для которых коэффициент корреляции примерно равен 0.
Рисунок 9 – Значения коэффициентов корреляции между переменными x11…x71 Т.о. необходимо исключить из рассмотрения переменные Total assets и Shareholders Return, тогда повторное обращение к функции View\Correlation Matrix даст отличные от нуля коэффициенты корреляции (рисунок 10).
Рисунок 10 - Расчёт коэффициентов корреляции между переменными x11…x51 Построим главные компоненты по сокращённому пространству исходных признаков x11…x15, выбрав пункт меню View\Principal Components и выбрав при помощи кнопки Select соответствующие переменные x11…x15 (рисунок 11).
Рисунок 11- Построение главных компонент для финансовой составляющей Полученные результаты моделирования представлены на рисунке 12. В таблице 5 приведены показатели и атрибуты окна результатов моделирования (рисунок 12).
Рисунок 12 – Окно результатов моделирования методом главных компонент Таблица 5 – Значения атрибутов и показателей окна, представленного на рисунке 12
Выберем главную компоненту PC1 (или y1) с максимальным собственным числом Eigenvalue ( Столбцы PCi показывают значения коэффициентов главных компонент wj= (w1j,...,wpj)', по данным столбца PC1 построим первую главную компоненту y1, формула (2).
где X11 - Net income, bln$ (Чистая прибыль, млрд. $); X21 - Sales&Revenues, bln$ (Выручка, млрд.$); X31 - Stockholders’ Equity, bln$ (Акционерный капитал, млдр.$); X41 - Gross cash, bln$ (Валовая наличность, млдр.$); X51 - Cash dividends, $ (Наличные дивиденды, $). Первое (наибольшее) значение столбца Eigenvalue рисунка 12 показывает абсолютный вклад Первое (наибольшее) значение столбца Proportion рисунка 12 показывает относительный вклад первой главной компоненты PC1 (или y1) равный 87,95% (=4.3977/(4.3977+0.3572+0.2288+0.0162+0.0000)*100%) в общую дисперсию наблюдаемых признаков X11 …X51, следовательно остальными главными компонентами PC2 … PC5 (с незначительными вкладами в общую дисперсию) можно пренебречь, а PC1 рассматривать как главную компоненту с наибольшей значимостью (весомостью). Тогда выбираем PC1 (или y1), формула (2), как первый элемент вектора функций Ford Motor Company, характеризующий финансовую составляющую устойчивого развития в целом, а соответствующее собственное число Сохраним новую переменную - главную компоненту y1 в созданном наборе данных Ford.gdt, нажав на знак “+” меню окна, представленного на рисунке 12, и кнопку ОК. Аналогичным описанному выше способу построим главные компоненты для остальных составляющих устойчивого развития «продукт и потребители» (y2), «качество отношений с персоналом» (y3), «окружающая среда и безопасность» (y4) и получим следующие значения, представленные формулами (3-5).
где X12 - Market share US, % (Доля рынка в США, %); X22 - Market share Europe (Доля рынка в США, %); X32 - Customer satisfaction, % (Удовлетворённость потребителя, %) X42 - Customer Loyalty, US % (Верность потребителя, США %) X52 - Vehicles sold, units (Объём продаж, шт.).
где X13 - Personnel full-time (Численность персонала на полной ставке,чел.); X23 – Employee satisfaction, % (Удовлетворённость работников, %); X33 - Laybor cost per hour, $ (З.пл. в час, $).
где X14 - Ford U.S. Corporate Average Fuel Economy (Экономия топлива, США, миль на галлон); X24 – Energy efficiency index, % (Индекс эффективности энергопотребления, %); X44 - Global Fatalities (Число смертельных случаев на производстве). Т.о. получен вектор функций а=( y1, y2, y3, y4 )',для предприятия Ford Motor Company. Нажав на пиктограмму системного калькулятора в нижнем левом углу стартового экрана Gretl (рисунок 3), рассчитаем общий рейтинг устойчивого развития Ford
|






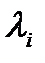 корреляционной матрицы, которое характеризует абсолютный вклад соответствующей главной компоненты
корреляционной матрицы, которое характеризует абсолютный вклад соответствующей главной компоненты  в суммарную дисперсию исходных признаков
в суммарную дисперсию исходных признаков 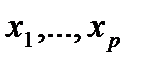 (весомость
(весомость  );
);
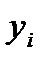
 ).
). (2)
(2) первой главной компоненты PC1 (или y1) в общую дисперсию наблюдаемых признаков X11 …X51.
первой главной компоненты PC1 (или y1) в общую дисперсию наблюдаемых признаков X11 …X51.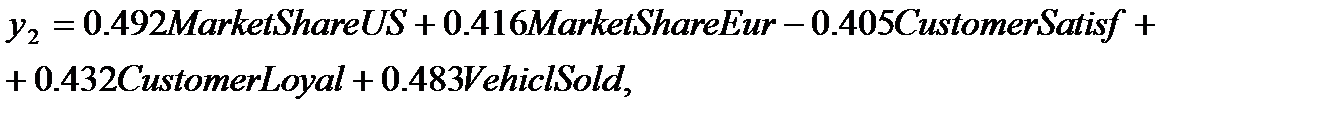 (3)
(3)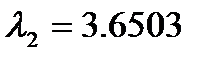 рейтинг составляющей «Продукт и потребители»;
рейтинг составляющей «Продукт и потребители»; (4)
(4) рейтинг составляющей «Качество отношений с персоналом»;
рейтинг составляющей «Качество отношений с персоналом»; (5)
(5) «Окружающая среда и безопасность»;
«Окружающая среда и безопасность»; как среднее арифметическое вышеперечисленных рейтингов отдельных составляющих. Данный показатель будем использовать для сопоставления значений рейтингов нескольких предприятий при сравнительном анализе их уровня устойчивого развития.
как среднее арифметическое вышеперечисленных рейтингов отдельных составляющих. Данный показатель будем использовать для сопоставления значений рейтингов нескольких предприятий при сравнительном анализе их уровня устойчивого развития.


