Оценивание гетероскедастичной модели с использованием взвешенного метода наименьших квадратов ВМНК (WLS)
Существует два способа реализации ВМНК (WLS) в пакете Gretl: 1. При выборе из главного меню команды Model\Other Linear Models\Weighted Least Squares ….(рисунок 12) открывается окно спецификации модели, которое предусматривает выбор из списка переменных открытого набора переменной - веса w. Данная переменная добавляется к набору путём ввода данных вручную или определяется путём ввода соответствующей формулы. Данный способ используется если дисперсия ошибки
где
Рисунок 12 – Способы реализации ВМНК (WLS) в пакете Gretl
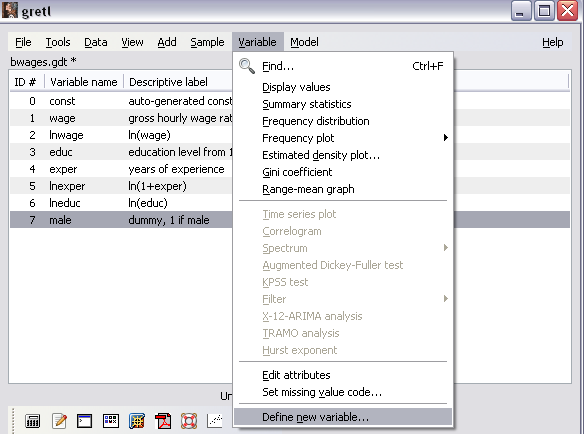
Обратимся к вышеприведённому примеру набора данных bwages.gdt для иллюстрации обоих способов оценивания регрессионной модели Этап 1. Введём новую переменную – вес w, которая будет определяться по формуле Для этого выберем команду Define new variable из меню Variable (рисунок 13).
Рисунок 13 – Создание новой переменной
В открывшемся окне “add var” введём имя переменной w и нажмём ОК, в появившемся окне «edit data» не вводим значения переменной, а нажимаем кнопку «close» для создания переменной с пустыми значениями (рисунок 14).
Рисунок 14 – Ввод имени переменной
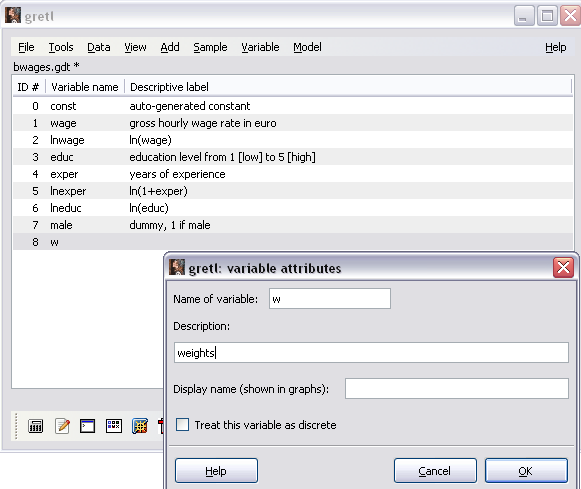
Данная переменная w c пустыми значениями и без описания появится в списке открытого набора данных. Введём описание переменной, обратившись к команде Variable\Edit Attributes. В открывшемся окне (рисунок 15) введём в поле “Description” описание «weights» (веса) и нажмём ОК.
Рисунок 15 – Изменение атрибутов переменной
Введём формулу для переменной w, повторно обратившись к команде Variable\Edit Attributes. Теперь в поле“Description” вместо описания «weights» введём формулу =1/(3*educ^2) (рисунок 16).
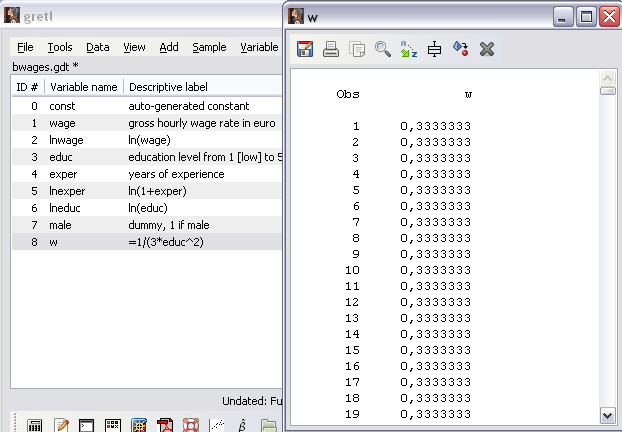
Рисунок 16 – Ввод формулы для определения переменной w Этап 2. Просмотрим значения созданной переменной w, выбрав её в списке щелчком мыши и обратившись к команде Data\Display Values (или двойным щелчком мыши по её названию в списке) (рисунок 17).
Рисунок 17 – Просмотр значений переменной w Этап 3. Для оценки модели
Рисунок 18 – Реализация ВМНК (OLS) в Gretl
Рисунок 19 – Оценивание модели Результаты оценивания представлены в окне результатов моделирования (рисунок 20).
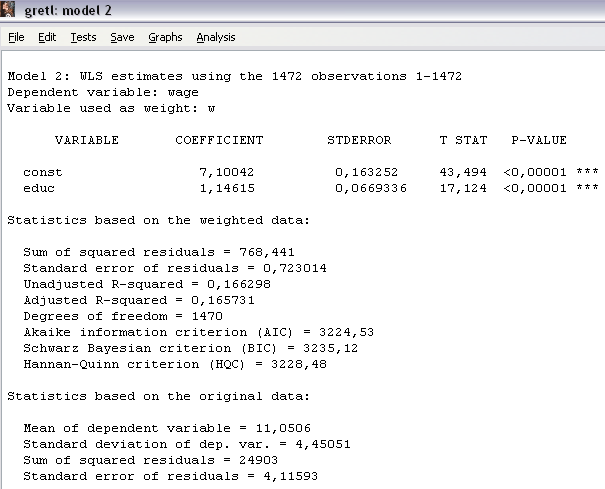
Рисунок 20 – Результаты оценивания модели Сравнивая модели, полученные методом ВМНК Этап 4. Воспользуемся вторым способом оценки модели
Рисунок 21 – Альтернативный способ оценки модели методом ВМНК (WLS)
Заполним окно спецификации также, как на предыдущем этапе за исключением ввода переменной – веса w, и нажмём кнопку ОК (рисунок 22).
Рисунок 22 – Оценивание модели
Сравнивая полученную модель
Рисунок 23 – Результаты оценивания модели
Проверим условие корректности применения рассматриваемого метода –получение нормального распределения остатков, - обратившись к команде Tests\normality of residual… меню окна модели (рисунок 23). Рисунок 24 показывает, что данное условие не соблюдается P-value=0,0000, что меньше уровней значимости 1% и 5%, поэтому отвергаем нулевую гипотезу о нормальности распределения остатков.
Вывод: В результате исследования 1479 бельгийских семей выявлена прямая зависимость заработной платы (wage) от уровня образования (educ). Наилучшей моделью, описывающей рассматриваемую зависимость, является модель
Рисунок 24 – Результаты теста на нормальность распределения остатков модели
|

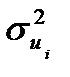 или известна или неизвестна, но существует соотношение между ней и одной из объясняющих переменных (
или известна или неизвестна, но существует соотношение между ней и одной из объясняющих переменных (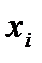 ), например,
), например,  .
.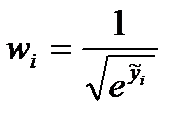 , (4)
, (4)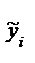 - модельные значения зависимой переменной, полученные при использовании 1МНК; e=2,718..; wi -вес i-го наблюдения.
- модельные значения зависимой переменной, полученные при использовании 1МНК; e=2,718..; wi -вес i-го наблюдения.
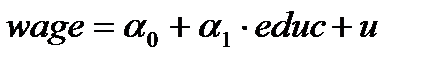 методом ВМНК.
методом ВМНК. .
.



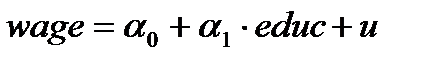 методом ВМНК (WLS)
методом ВМНК (WLS) (рисунок 20) и методом 1МНК
(рисунок 20) и методом 1МНК 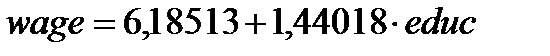 (рисунок 7) можно сделать вывод о том, что при использовании 1МНК оценка коэффициента
(рисунок 7) можно сделать вывод о том, что при использовании 1МНК оценка коэффициента 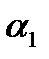 была завышена, а оценки
была завышена, а оценки 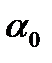 и T-STAT – занижены, но на правильности решения о принятии альтернативной гипотезы это не отразилось (значения P-VALUE не изменились).
и T-STAT – занижены, но на правильности решения о принятии альтернативной гипотезы это не отразилось (значения P-VALUE не изменились).

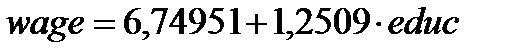 (рисунок 23) с моделью, оцененною с применением 1МНК
(рисунок 23) с моделью, оцененною с применением 1МНК 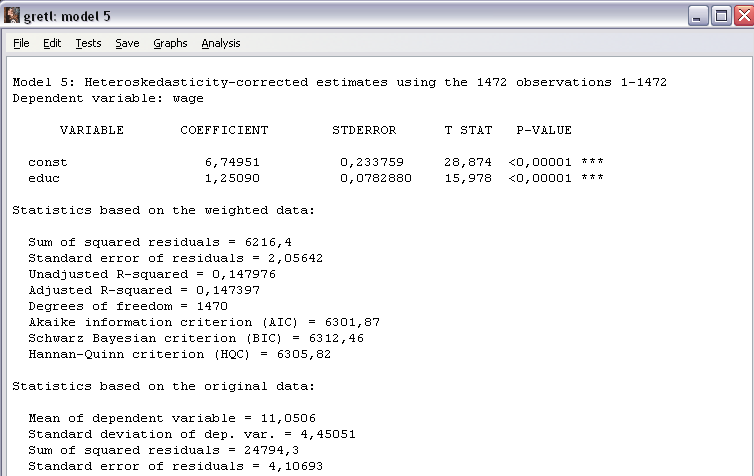
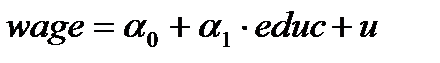 методом ВМНК (WLS) с автоматическим определением весов наблюдений
методом ВМНК (WLS) с автоматическим определением весов наблюдений




